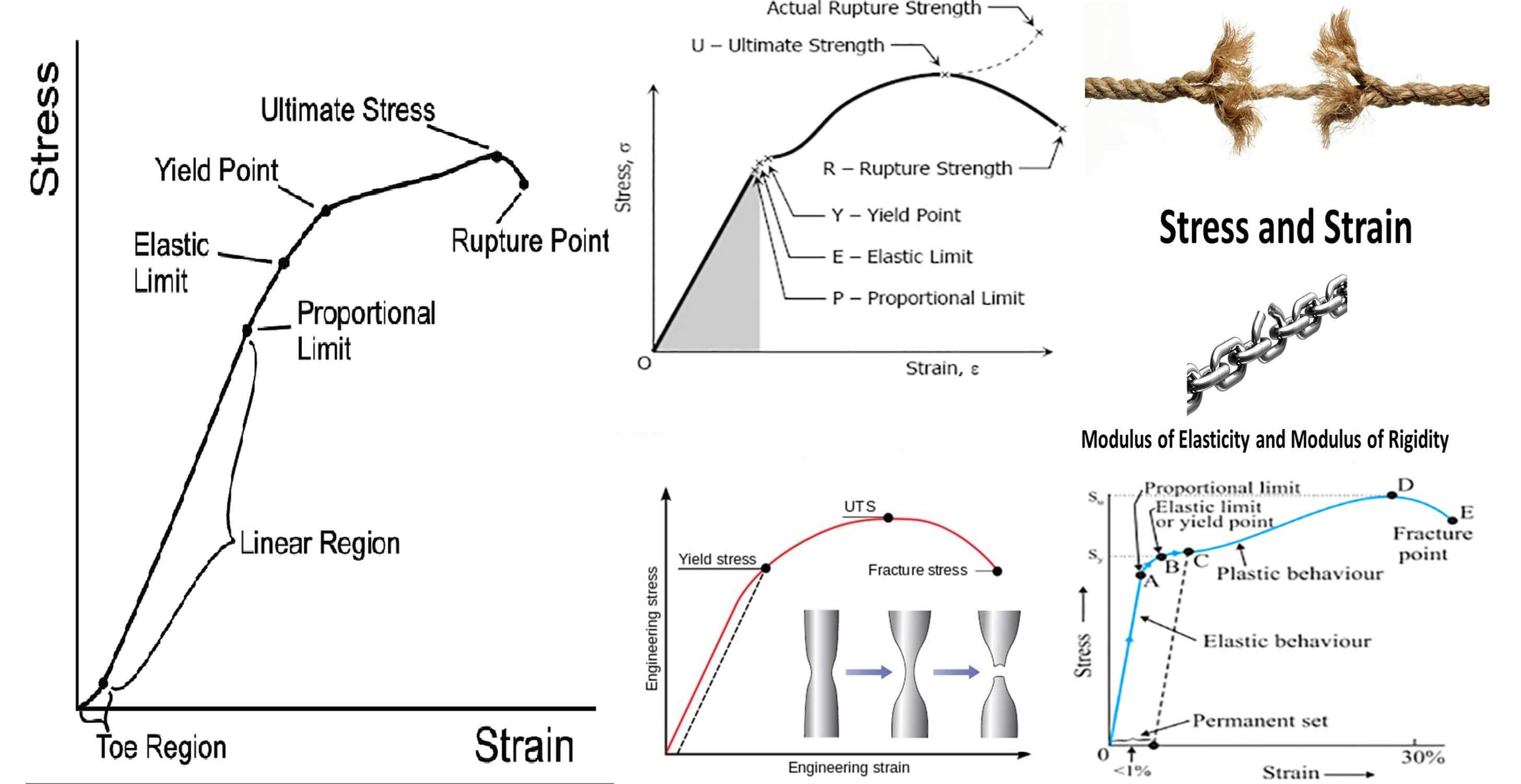
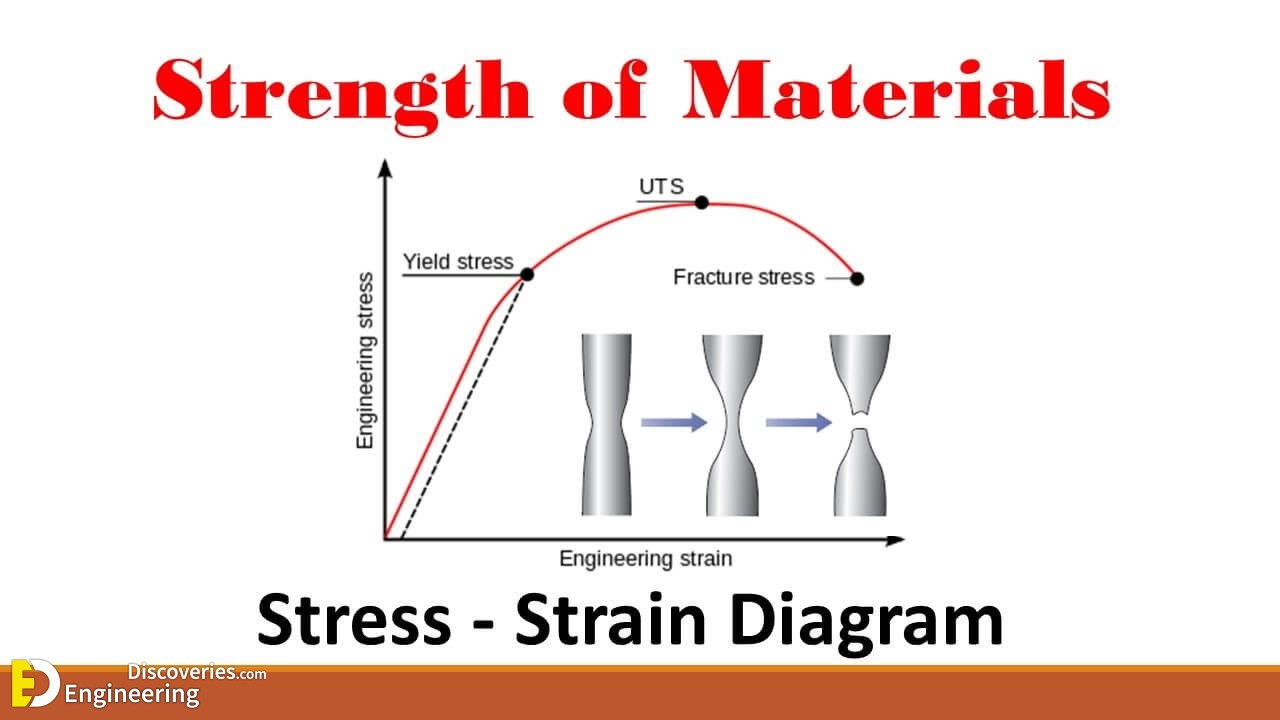
Suppose that a metal specimen be placed in tension-compression-testing machine. As the axial load is gradually increased in increments, the total elongation over the gauge length is measured at each increment of the load and this is continued until failure of the specimen takes place. Knowing the original cross-sectional area and length of the specimen, the normal stress σ and the strain ε can be obtained. The graph of these quantities with the stress σ along the y-axis and the strain ε along the x-axis is called the stress-strain diagram. The stress – strain diagram differs in form for various materials.
Metallic engineering materials are classified as either ductile or brittle materials. A ductile material is one having relatively large tensile strains up to the point of rupture like structural steel and aluminum, whereas brittle materials has a relatively small strain up to the point of rupture like cast iron and concrete. An arbitrary strain of 0.05 mm/mm is frequently taken as the dividing line between these two classes.
Stress
If an applied force causes a change in the dimension of the material, then the material is in the state of stress. If we divide the applied force (F) by the cross-sectional area (A), we get the stress. The symbol of stress is σ (Greek letter sigma). For tensile (+) and compressive (-) forces. The standard international unit of stress is the pascal (Pa), where 1 Pa = 1 N/m2. The formula to derive the stress number is σ = F/A. For tensile and compressive forces, the area taken is perpendicular to the applied force. For sheer force, the area is taken parallel to the applied force. The symbol for shear stress is tau (τ).
Strain
Strain is the change in the dimension (L-L0) with respect to the original. It is denoted by the symbol epsilon (ε). The formula is ε = (L-L0) / L0. For a shear force, strain is expressed by γ (gamma)
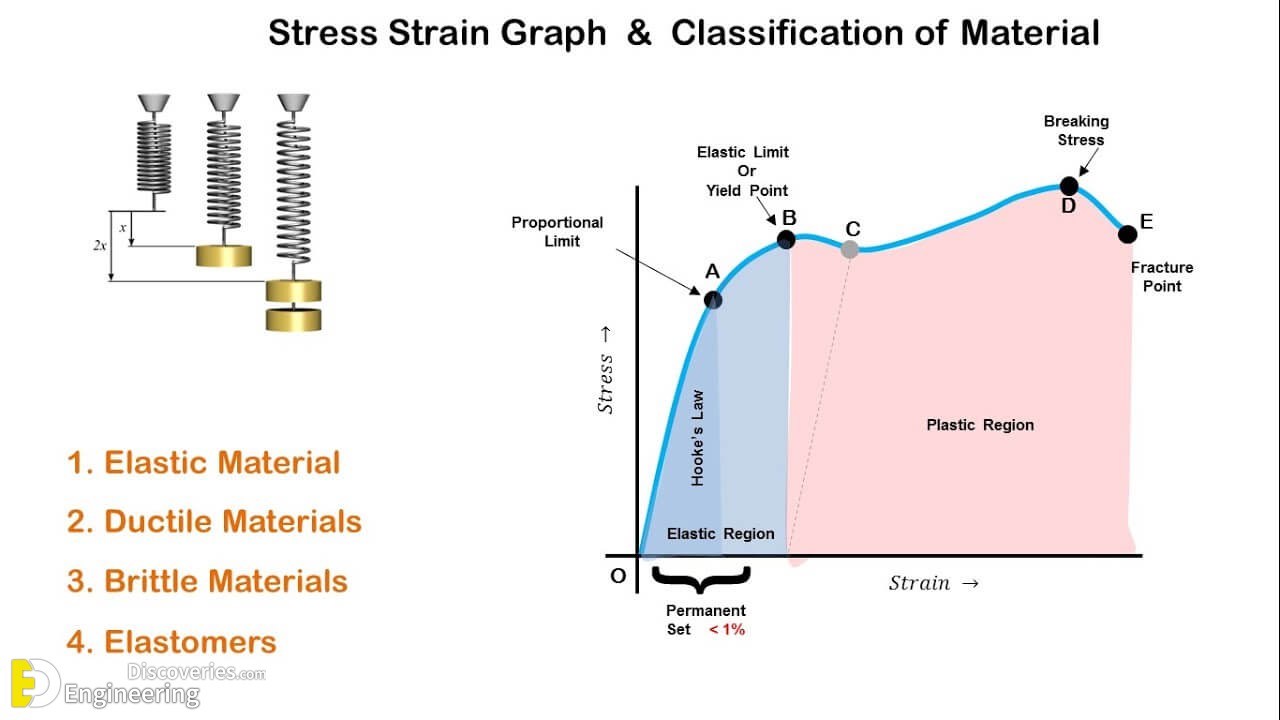
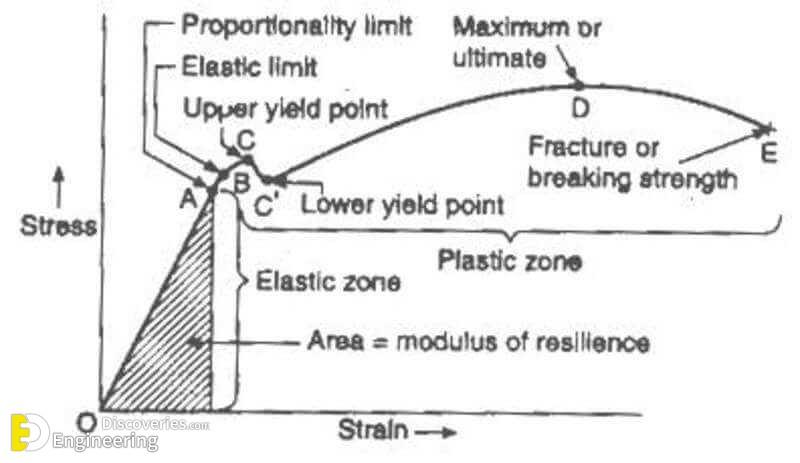
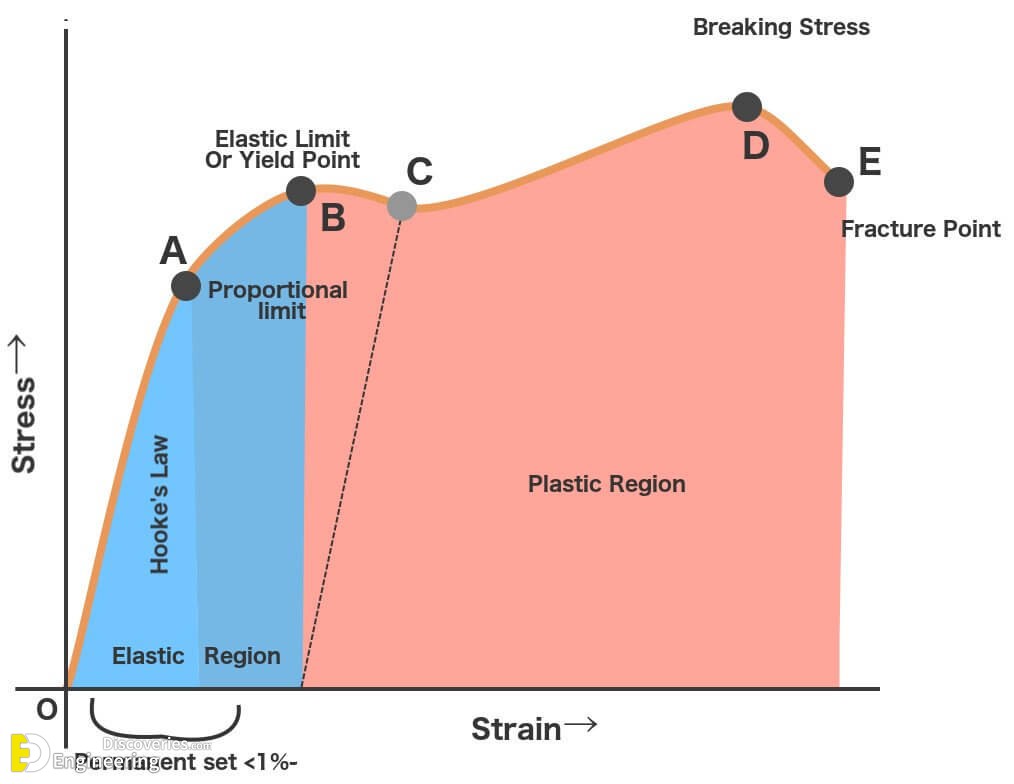
Proportional Limit (Hooke’s Law)
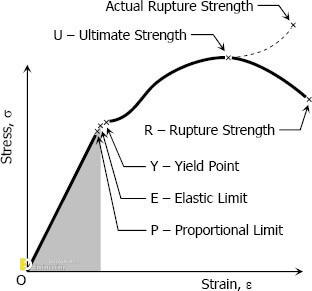
From the origin O to the point called proportional limit, the stress-strain curve is a straight line. This linear relation between elongation and the axial force causing was first noticed by Sir Robert Hooks in 1678 and is called Hooke’s Law that within the proportional limit, the stress is directly proportional to strain or
The constant of proportionality k is called the Modulus of Elasticity E or Young′s Modulus and is equal to the slope of the stress-strain diagram from O to P. Then
(The modulus of elasticity (= Young’s modulus) E is a mechanical property that measures the stiffness of a solid material. It defines the relationship between stress (force per unit area) and strain(proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation.)
Elastic Limit (Elasticity limit)
Elastic limit is the limiting value of stress up to which the material is perfectly elastic. From the curve, point E is the elastic limit point. Material will return back to its original position, If it is unloaded before the crossing of point E. This is so, because material is perfectly elastic up to point E.
Plasticity Limit
This is a property that allows the material to remain deformed without fracture even after the force is removed.
Yield Point
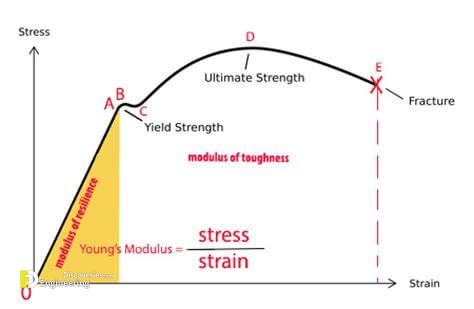
Yield stress is defined as the stress after which material extension takes place more quickly with no or little increase in load. Point Y is the yield point on the graph and stress associated with this point is known as yield stress.
Ultimate Strength (Ultimate stress point)
Ultimate stress point is the maximum strength that material have to bear stress before breaking. It can also be defined as the ultimate stress corresponding to the peak point on the stress strain graph. On the graph point U is the ultimate stress point. After point U material have very minute or zero strength to face further stress.
Rapture Strength(Breaking point or breaking stress)
Breaking point or breaking stress is point where strength of material breaks. The stress associates with this point known as breaking strength or rupture strength. On the stress strain curve, point B is the breaking stress point.
Modulus of Resilience
Modulus of resilience is the work done on a unit volume of material as the force is gradually increased from O to P, in N·m/m3. This may be calculated as the area under the stress-strain curve from the origin O to up to the elastic limit E (the shaded area in the figure). The resilience of the material is its ability to absorb energy without creating a permanent distortion.
Modulus of Toughness
Modulus of toughness is the work done on a unit volume of material as the force is gradually increased from O to R, in N·m/m3. This may be calculated as the area under the entire stress-strain curve (from O to R). The toughness of a material is its ability to absorb energy without causing it to break.
Working Stress, Allowable Stress, and Factor of Safety
Working stress is defined as the actual stress of a material under a given loading. The maximum safe stress that a material can carry is termed as the allowable stress. The allowable stress should be limited to values not exceeding the proportional limit. However, since proportional limit is difficult to determine accurately, the allowable tress is taken as either the yield point or ultimate strength divided by a factor of safety. The ratio of this strength (ultimate or yield strength) to allowable strength is called the factor of safety.
For more information watch this video