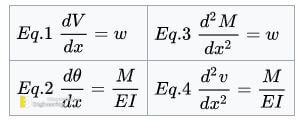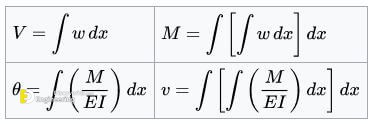Conjugate beam is defined as the imaginary beam with the same dimensions (length) as that of the original beam but load at any point on the conjugate beam is equal to the bending moment at that point divided by EI. The conjugate-beam method is an engineering method to derive the slope and displacement of a beam.
The conjugate-beam method was developed by H. Müller-Breslau in 1865. Essentially, it requires the same amount of computation as the moment-area theorems to determine a beam’s slope or deflection; however, this method relies only on the principles of statics, so its application will be more familiar. The basis for the method comes from the similarity of Eq. 1 and Eq 2 to Eq 3 and Eq 4. To show this similarity, these equations are shown below.
Integrated, the equations look like this.
Here the shear V compares with the slope θ, the moment M compares with the displacement v, and the external load w compares with the M/EI diagram. Below is a shear, moment, and deflection diagram. A M/EI diagram is a moment diagram divided by the beam’s Young’s modulus and moment of inertia.
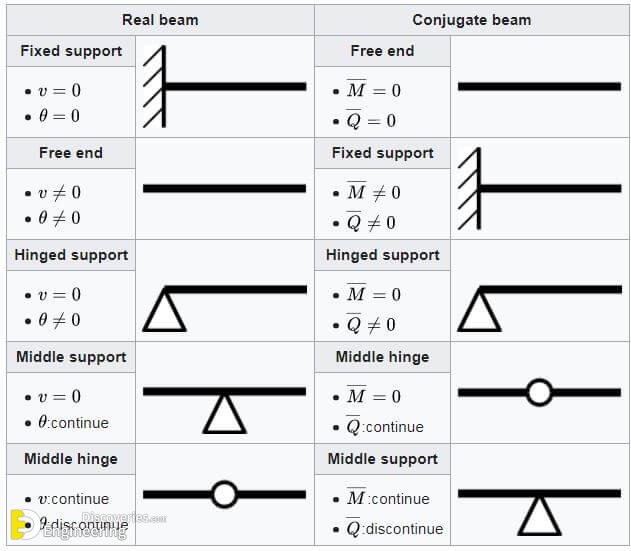
Conjugate-beam supports
Conjugate beam
1- Draw the conjugate beam for the real beam. This beam has the same length as the real beam and has corresponding supports as listed above.
2- In general, if the real support allows a slope, the conjugate support must develop shear; and if the real support allows a displacement, the conjugate support must develop a moment.
3- The conjugate beam is loaded with the real beam’s M/EI diagram. This loading is assumed to be distributed over the conjugate beam and is directed upward when M/EI is positive and downward when M/EI is negative. In other words, the loading always acts away from the beam.
Equilibrium
1- Using the equations of statics, determine the reactions at the conjugate beams supports.
2- Section the conjugate beam at the point where the slope θ and displacement Δ of the real beam is to be determined. At the section show the unknown shear V’ and M’ equal to θ and Δ, respectively, for the real beam. In particular, if these values are positive, and the slope is counterclockwise and the displacement is upward.
For more information watch this video