Geometry is the mathematical foundation upon which the physical world is interpreted and modeled. From architectural blueprints to modern electronics and design engineering, geometric principles are embedded in nearly everything. In this comprehensive guide, we explore the most essential geometric formulas and principles related to shapes and solids, providing a rich educational resource for students, educators, and professionals alike.
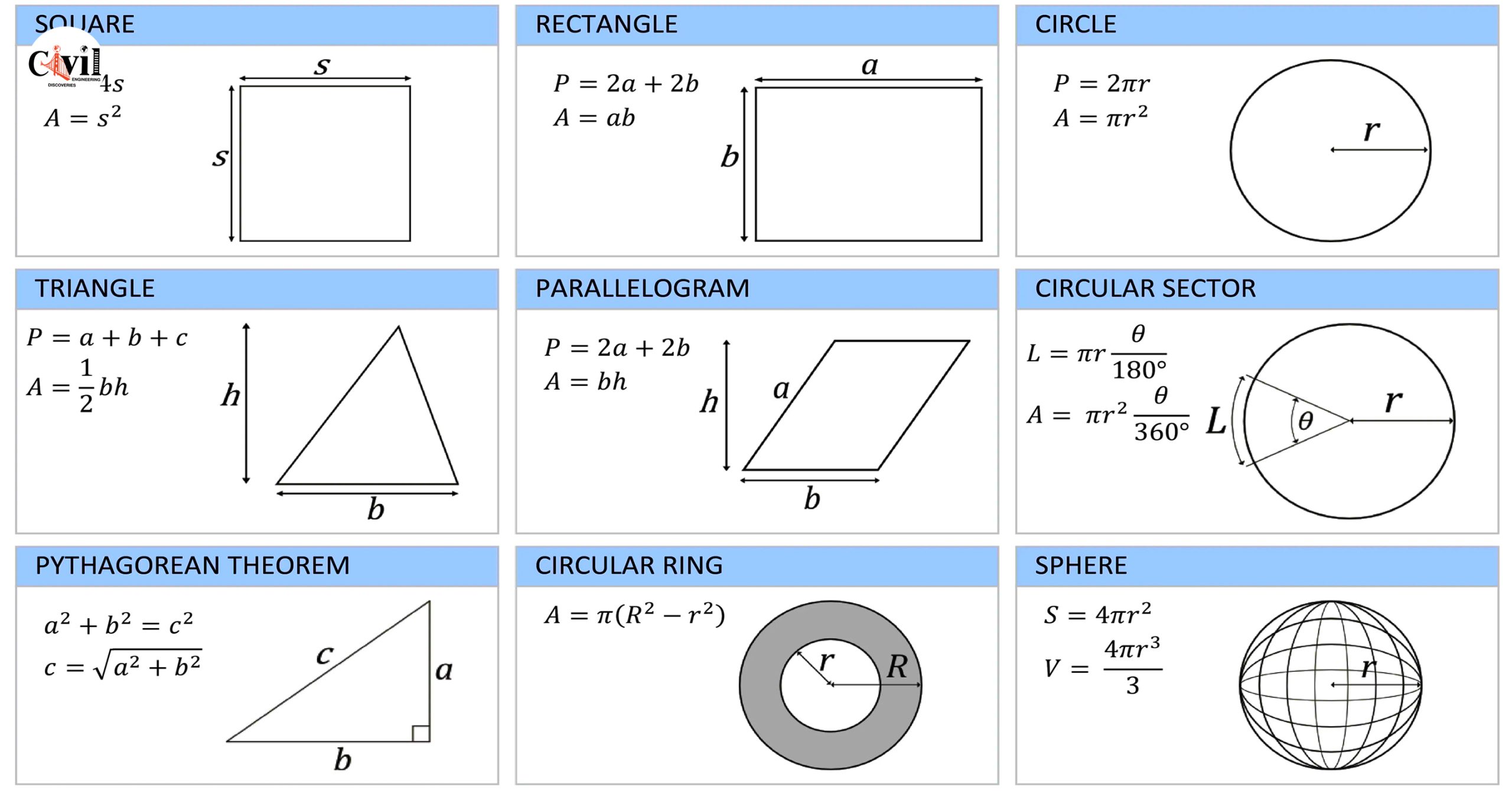
Understanding 2D Shapes: Definitions and Key Formulas
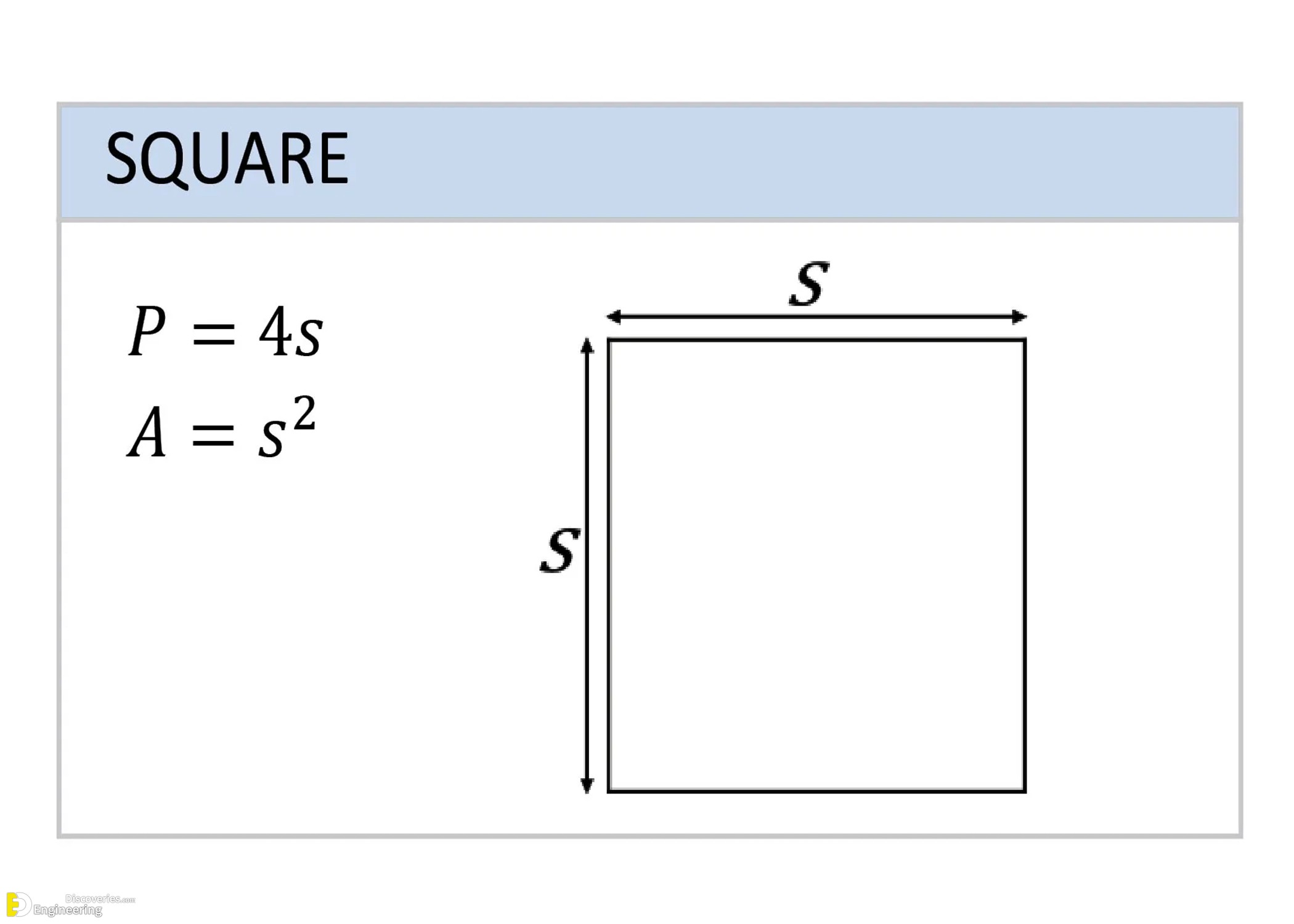
Square
A square is a regular quadrilateral with four equal sides and angles.
Perimeter (P) = 4s
Area (A) = s²
Where s is the length of one side.
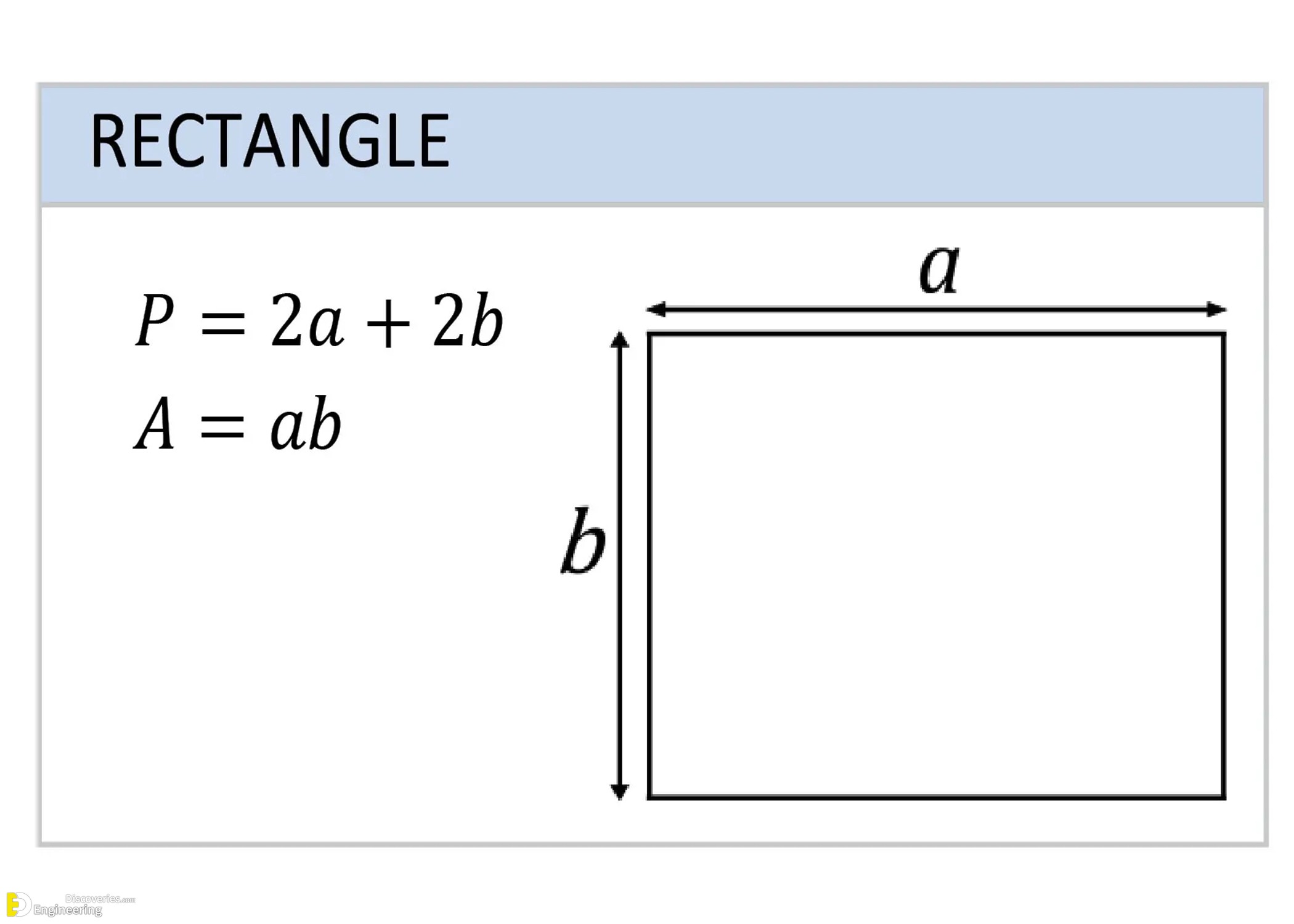
Rectangle
A rectangle has opposite sides equal and all angles right angles.
Perimeter (P) = 2a + 2b
Area (A) = ab
Where a and b are the lengths of adjacent sides.
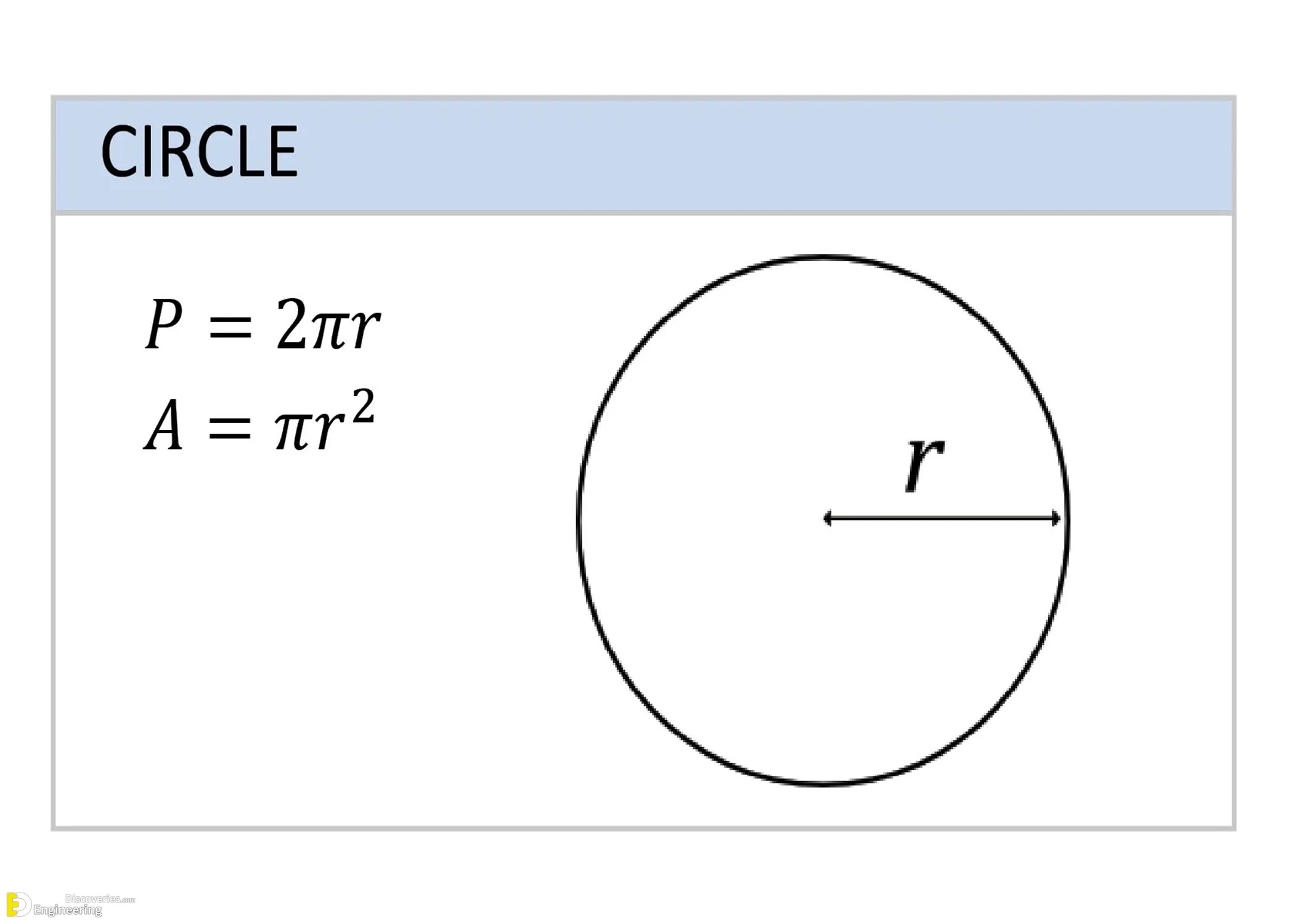
Circle
The circle is defined by its radius r, the distance from the center to any point on the edge.
Perimeter/Circumference (P) = 2πr
Area (A) = πr²
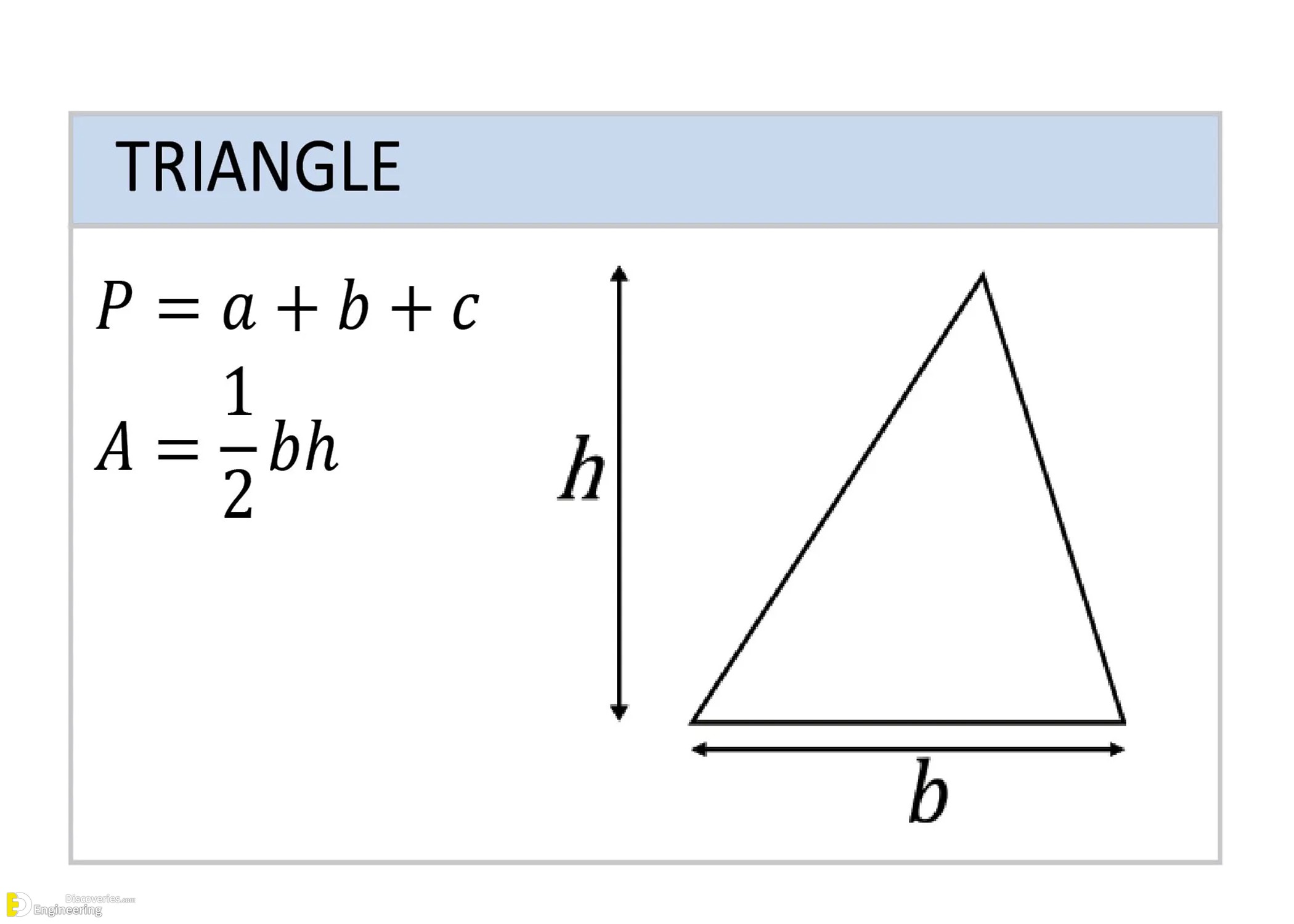
Triangle
Triangles vary in type but universally follow:
Perimeter (P) = a + b + c
Area (A) = (1/2)bh
Where a, b, and c are side lengths, and h is the height relative to base b.
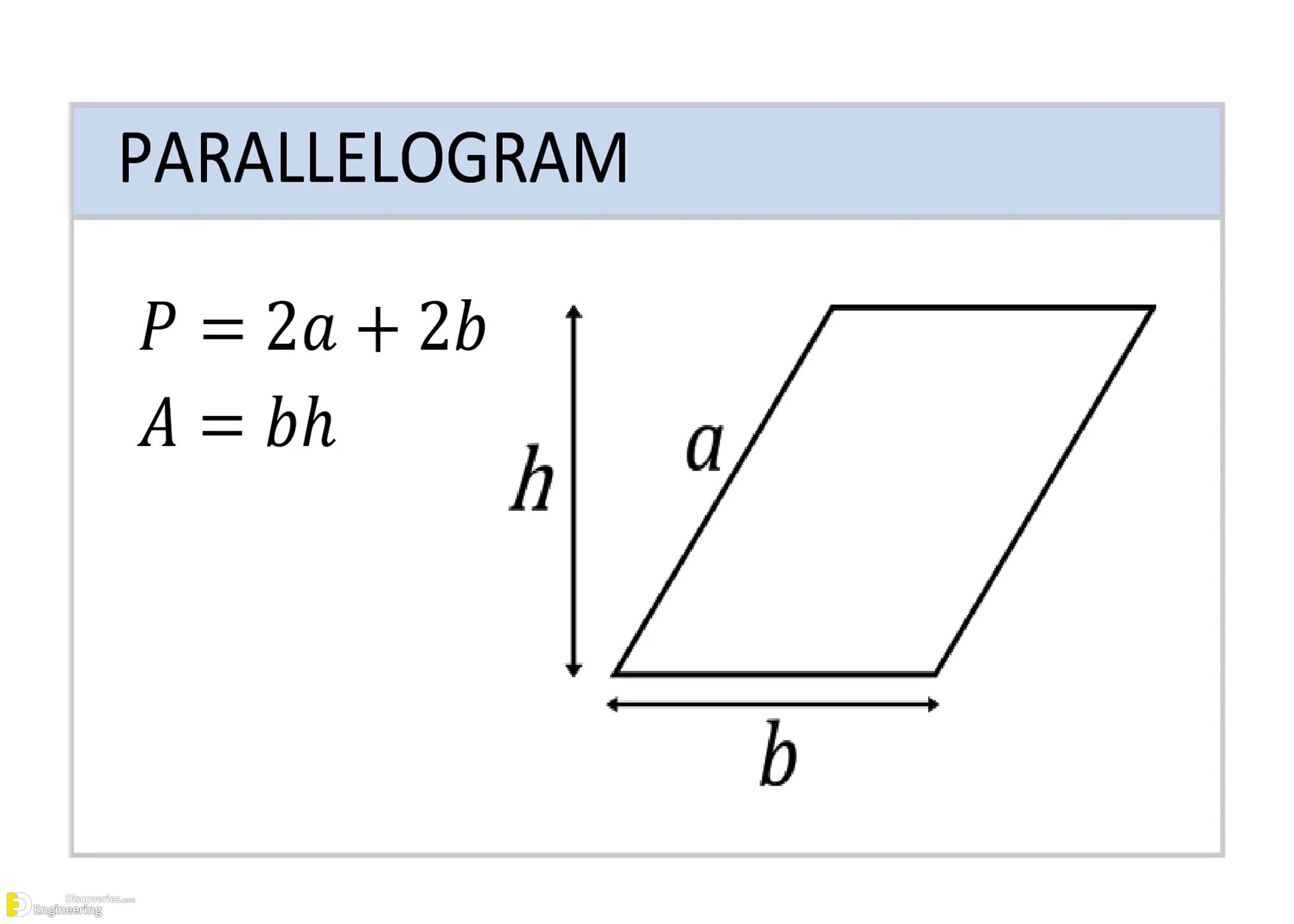
Parallelogram
A four-sided shape with opposite sides parallel and equal.
Perimeter (P) = 2a + 2b
Area (A) = bh
Where b is base and h is the perpendicular height.
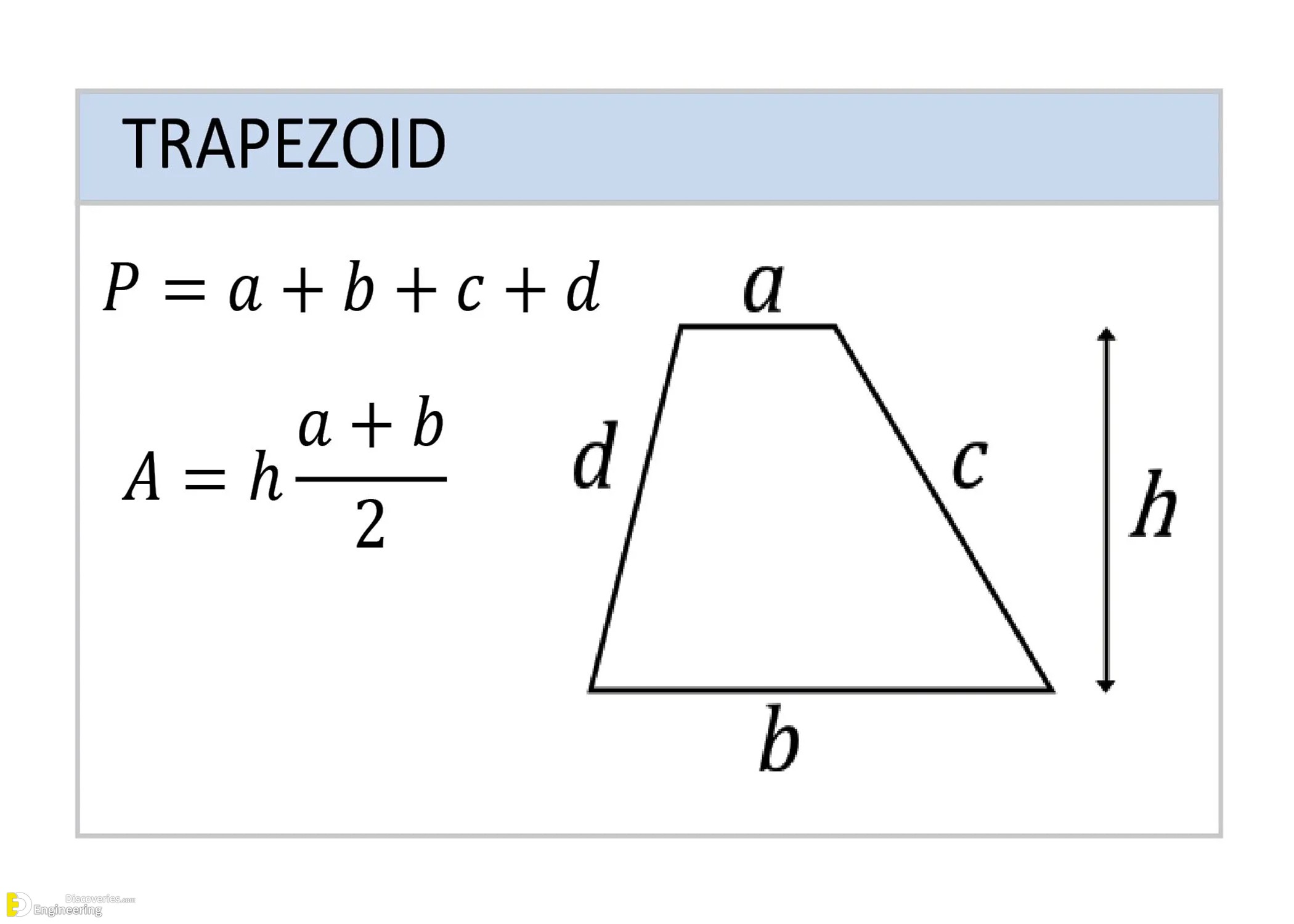
Trapezoid
A trapezoid has one pair of parallel sides.
Perimeter (P) = a + b + c + d
Area (A) = h × (a + b) / 2
Where a and b are the lengths of the parallel sides.
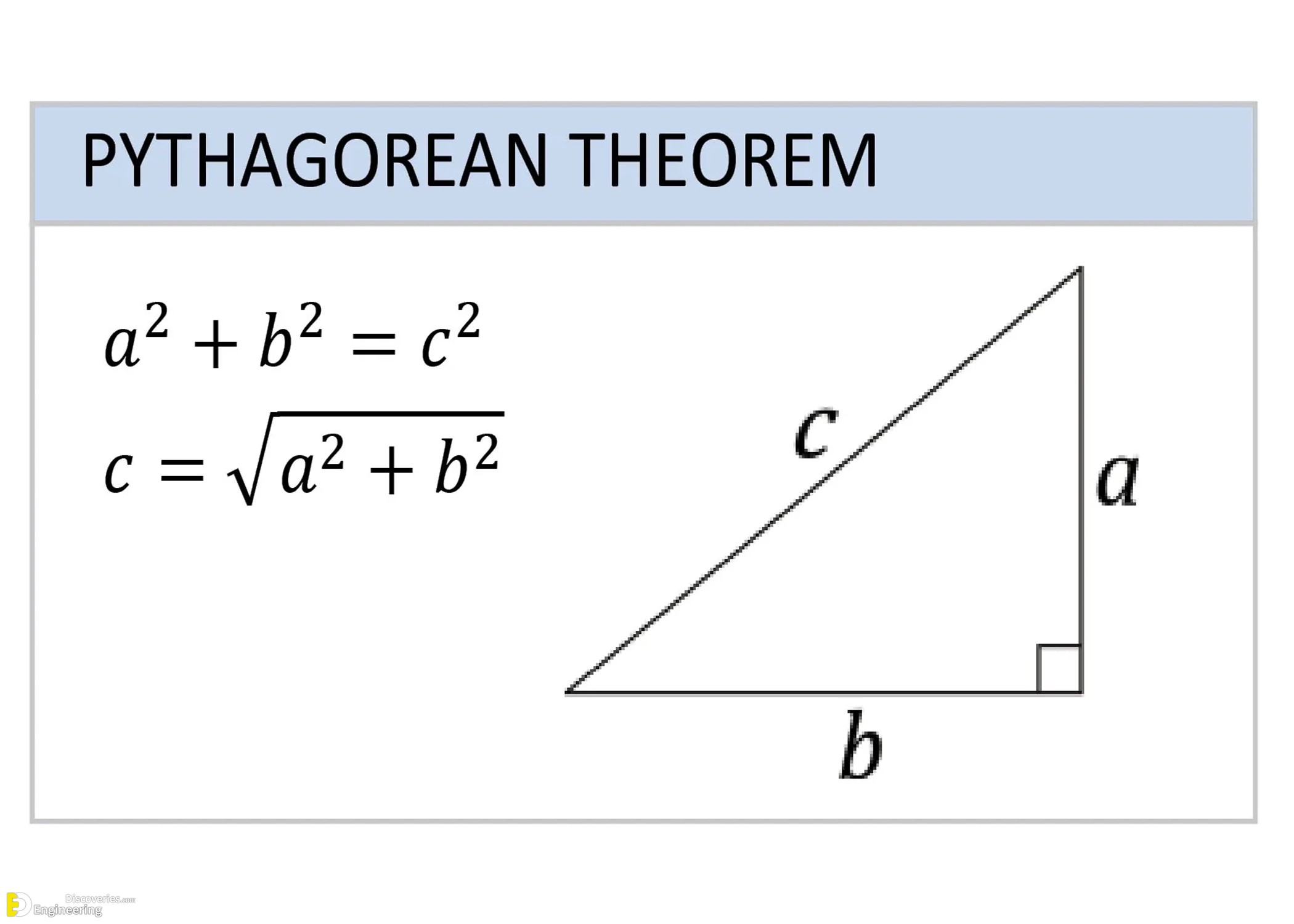
Pythagorean Theorem
Applicable to right-angled triangles:
c² = a² + b²
Therefore, c = √(a² + b²)
This is essential in solving diagonal lengths and triangulated measurements.
Advanced Circular Geometry
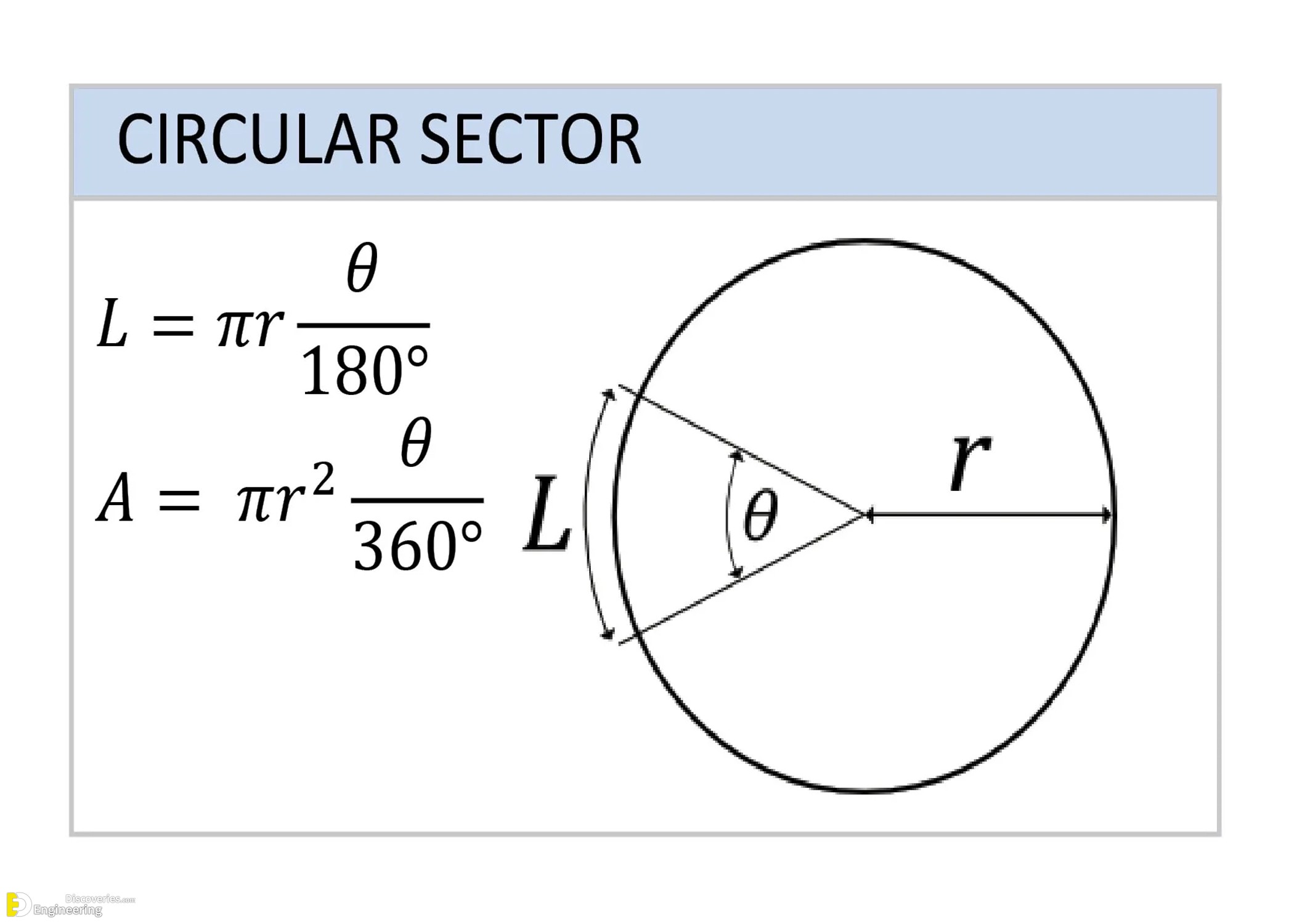
Circular Sector
A sector is a ‘slice’ of a circle, defined by a central angle θ.
Arc Length (L) = (θ / 180°) × πr
Area (A) = (θ / 360°) × πr²
Where θ is in degrees and r is the radius.
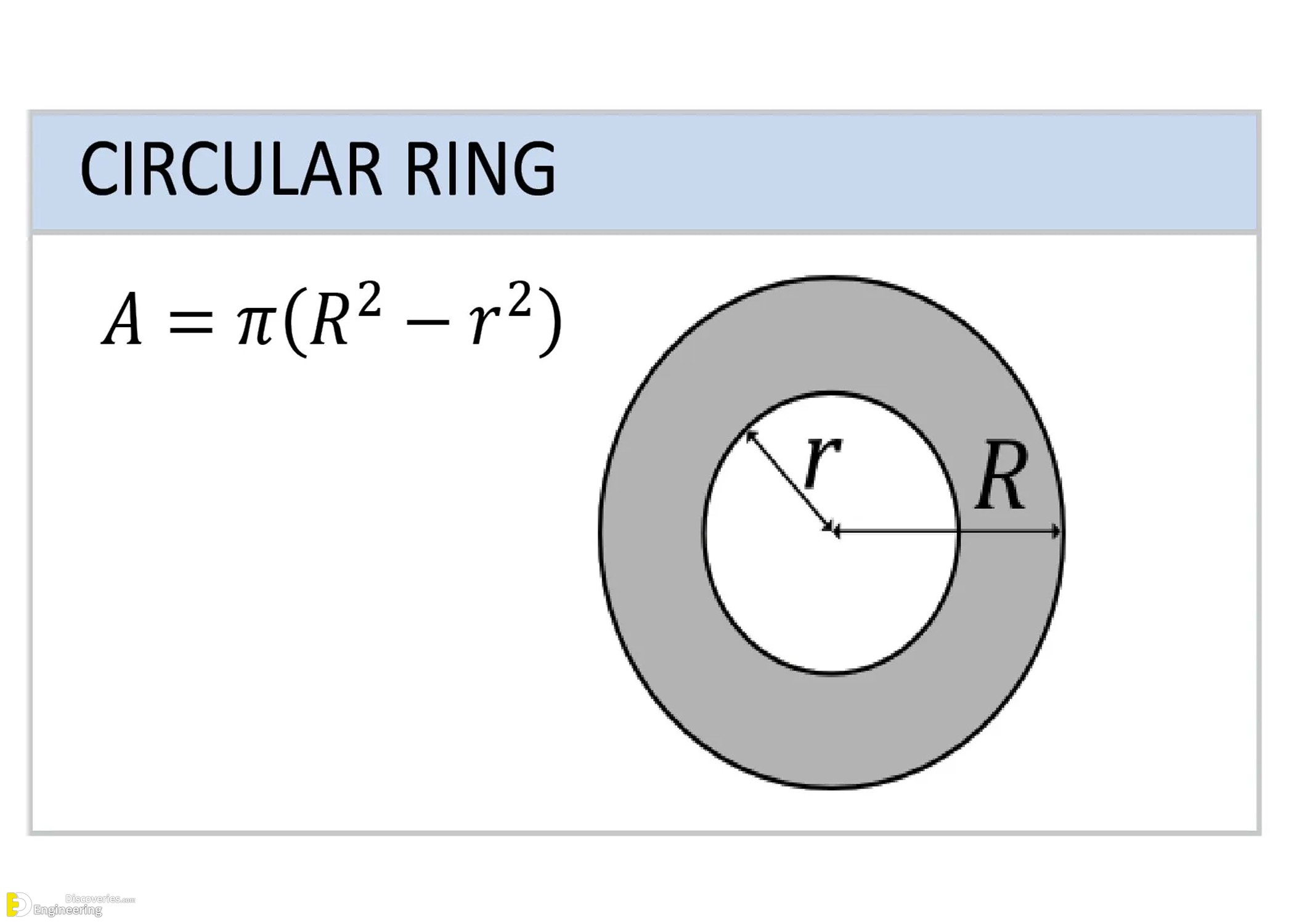
Circular Ring (Annulus)
Formed between two concentric circles.
Area (A) = π(R² – r²)
Where R is the outer radius and r is the inner radius.
3D Geometric Solids and Volume Formulas
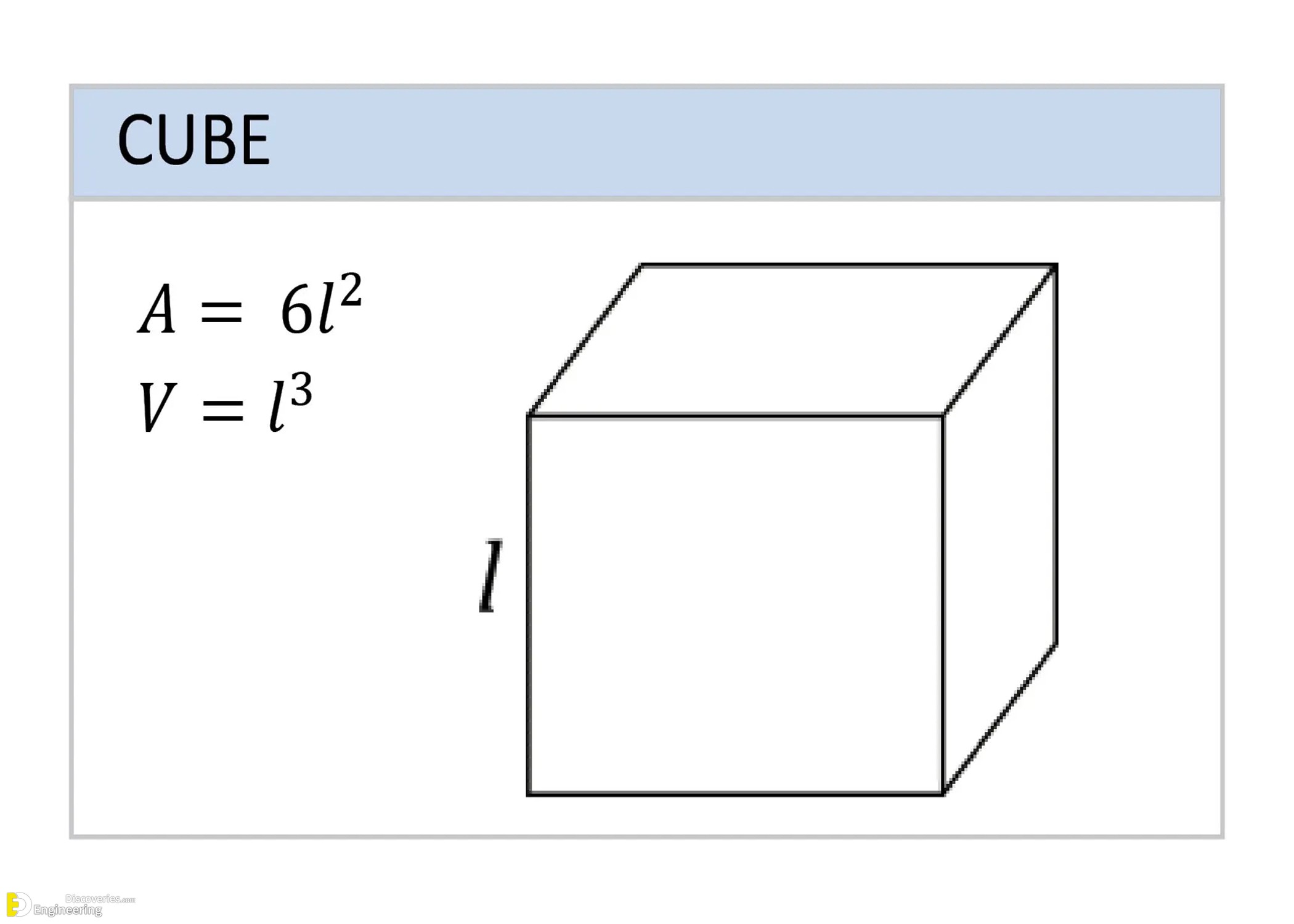
Cube
A cube has equal sides on all faces.
Surface Area (A) = 6l²
Volume (V) = l³
Where l is the edge length.
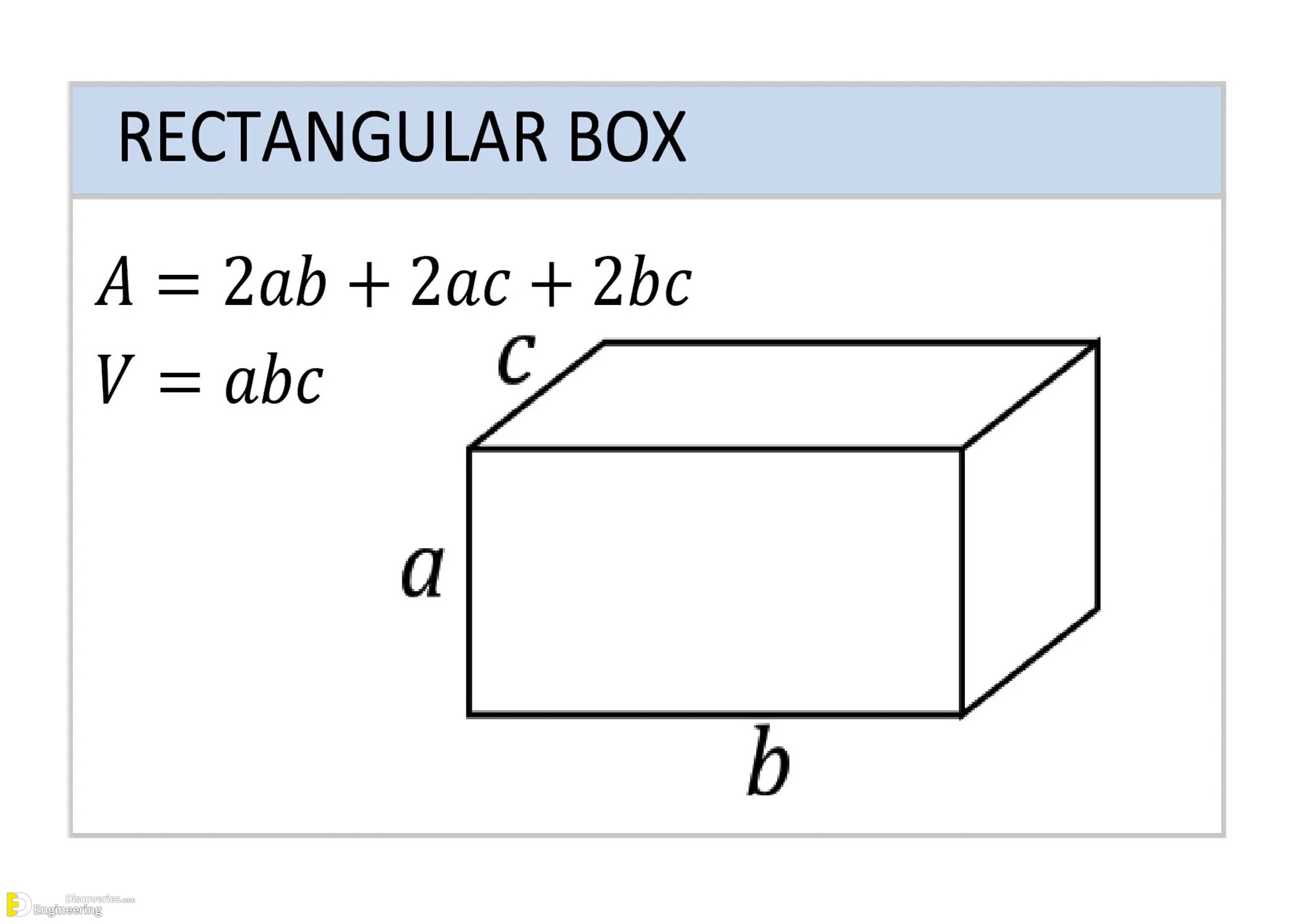
Rectangular Box (Cuboid)
Used extensively in packaging and construction.
Surface Area (A) = 2(ab + ac + bc)
Volume (V) = abc
Where a, b, and c are the lengths of the sides.
Sphere
A perfectly round geometrical object in 3D space.
Surface Area (S) = 4πr²
Volume (V) = (4/3)πr³
Where r is the radius.
Cylinder
Common in mechanical and architectural designs.
Surface Area (A) = 2πr(r + h)
Volume (V) = πr²h
Where r is the base radius, h is the height.
Right Circular Cone
A cone with a circular base and a pointed top.
Surface Area (A) = πr² + πrs
Slant Height (s) = √(r² + h²)
Volume (V) = (1/3)πr²h
Where r is base radius and h is vertical height.
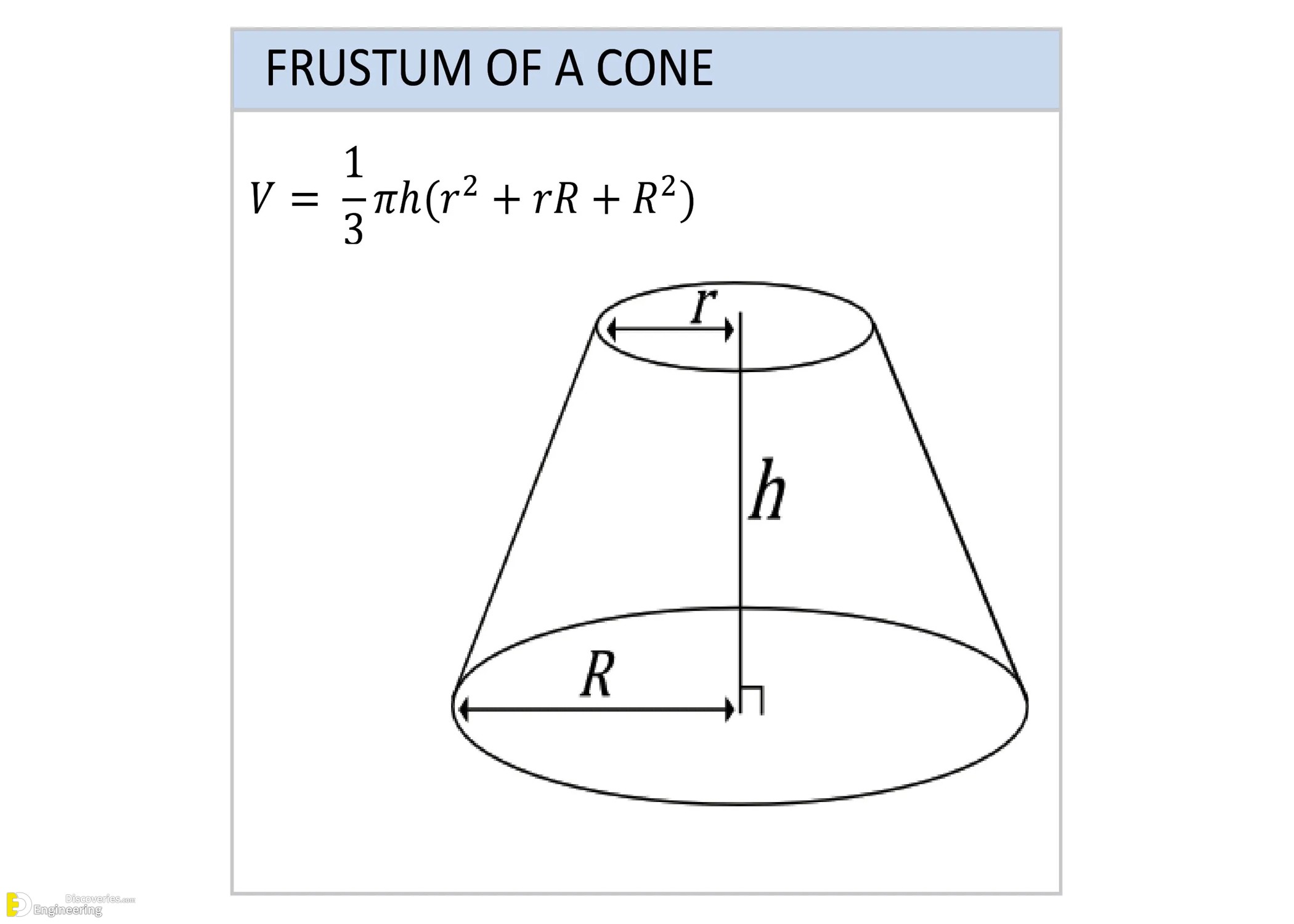
Frustum of a Cone
Created when a smaller cone is cut off from a larger cone.
Volume (V) = (1/3)πh(r² + rR + R²)
Where r and R are the radii of the two circular faces, and h is the height.
Practical Applications of Geometry in Real Life
Architecture and Construction
Geometry ensures precision in architectural blueprints. Rectangular and triangular calculations allow for strong, stable building designs, while the volume and surface area of shapes like cylinders and cones help in materials estimation.
Engineering and Design
Geometric principles are essential in civil, mechanical, and electrical engineering. For example, circular sector calculations are vital in designing turbines and gears, while volumes of cylinders and spheres are used to design tanks, pistons, and domes.
Electronics and PCB Design
In electronics, geometry is crucial in layout planning for Printed Circuit Boards (PCBs), ensuring optimal space usage and signal flow.
Everyday Calculations
Geometry is present in everyday decision-making, from calculating how much paint a room needs (using the area of walls) to estimating how much water a cylindrical tank can hold (using the volume of a cylinder).
Tips for Memorizing Geometric Formulas
Visualize: Associate each formula with its diagram.
Group Similar Shapes: Recognize formulas’ similarities (e.g., cylinder volume vs. cone).
Use Mnemonics: Create short phrases to remember relationships, like “All Circles Are Pretty Round” for Area = πr², Perimeter = 2πr.
Practice: Solve a variety of problems regularly to internalize the concepts.
Why Geometry is Essential in Education and Industry
Geometry builds critical thinking and analytical skills, which are crucial in science, technology, engineering, and mathematics (STEM) fields. A solid grasp of geometric formulas allows for efficient problem-solving and innovation.
Educators leverage these formulas to prepare students for standardized tests and higher education, while professionals apply them in CAD software, simulations, and design schematics.