Dimensional Analysis: A Complete Guide

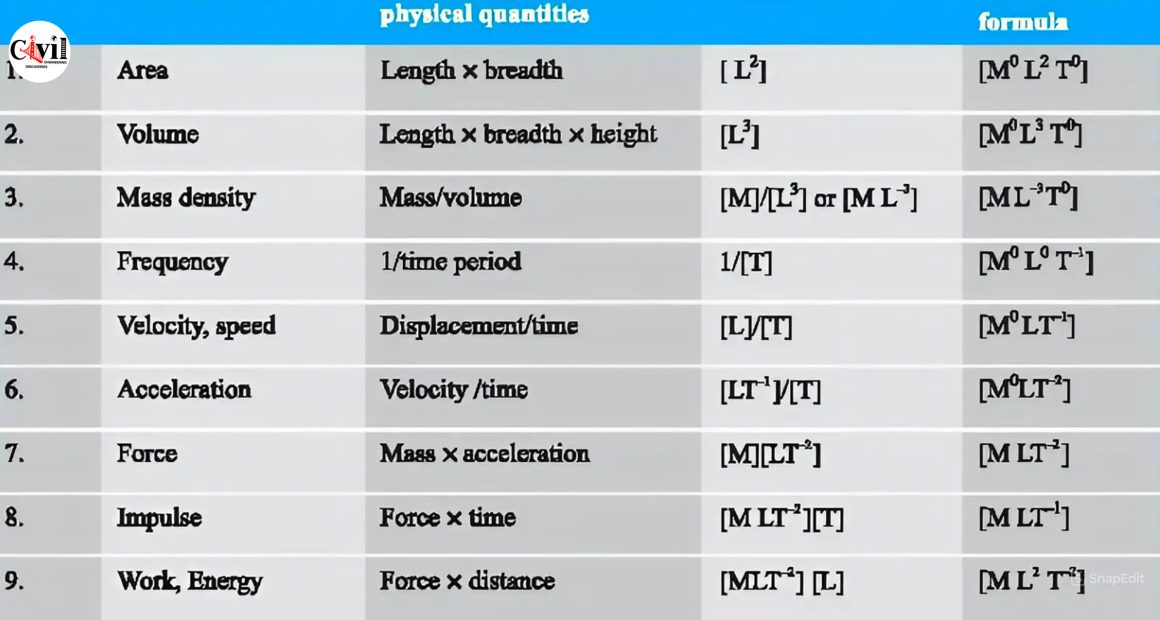
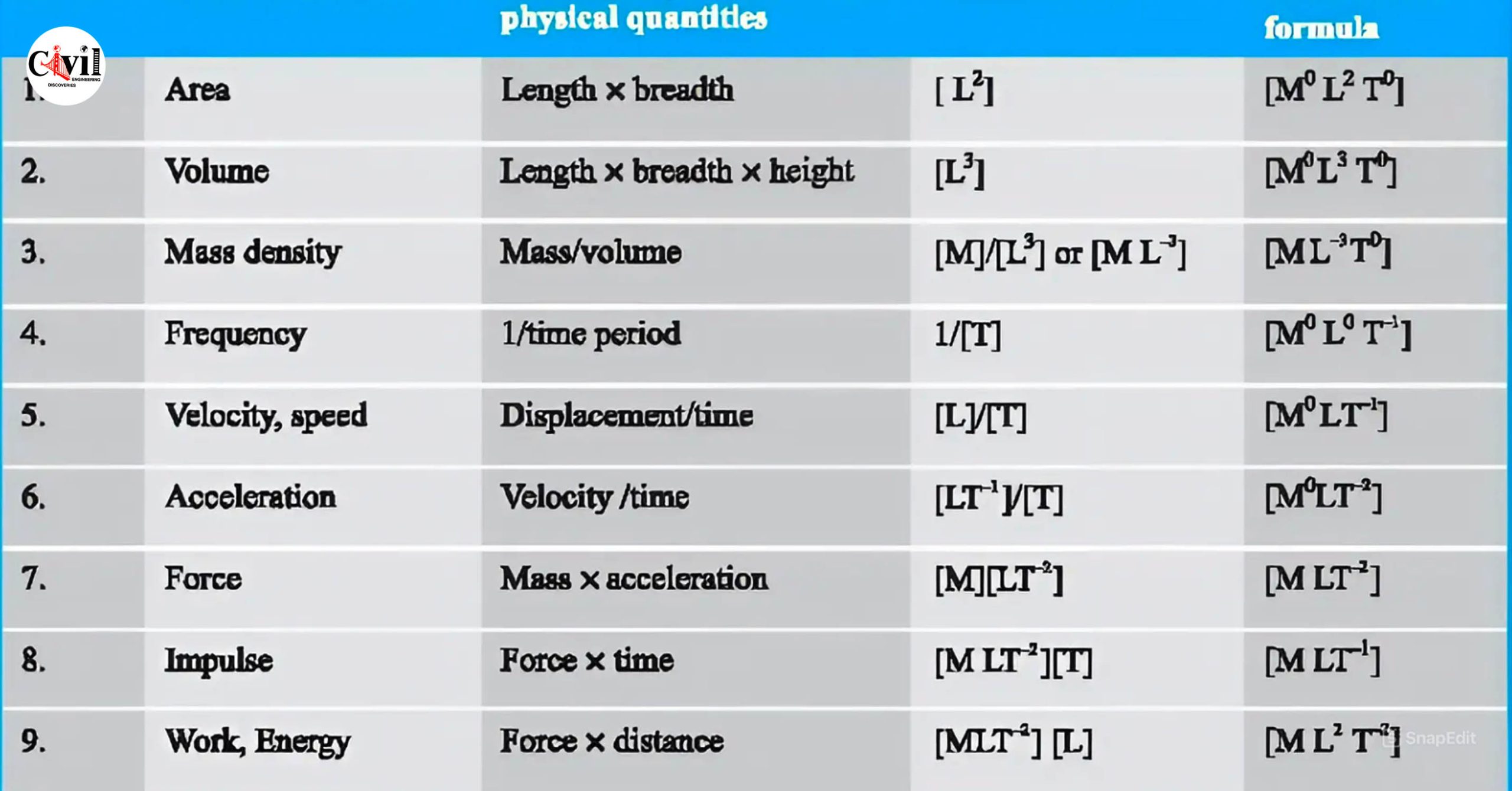
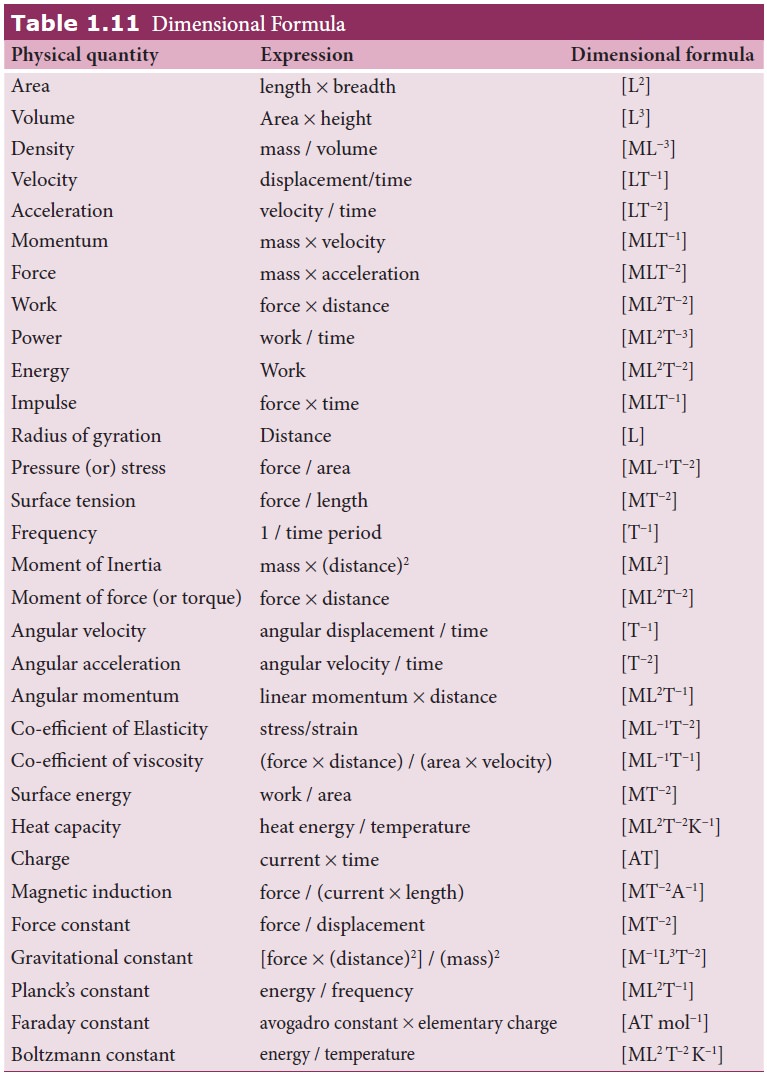
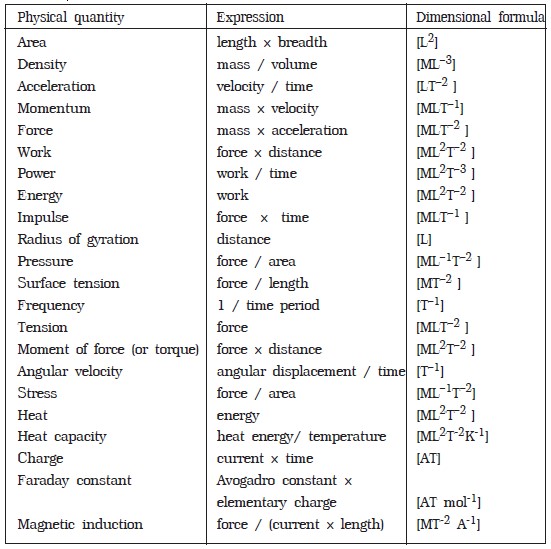
What is Dimensional Analysis?

Dimensional analysis is a method used to simplify complex equations and ensure consistency in physical calculations. By analyzing the dimensions of physical quantities, you can confirm the correctness of mathematical models and their units.

Importance of Dimensional Analysis

1. Verifying Equations
   Dimensional analysis helps verify whether equations are dimensionally consistent. If units match on both sides, the equation is likely correct.
2. Simplifying Problems
   It reduces the complexity of problems by identifying relationships between variables. This saves time and ensures precision.
3. Deriving Formulas
   Using this method, scientists and engineers derive formulas without requiring extensive experimentation.

Basic Principles of Dimensional Analysis

1. Fundamental Quantities
   The primary dimensions include mass (M), length (L), time (T), and electric current (I). These form the foundation for all physical quantities.
2. Dimensional Homogeneity
   All terms in a valid physical equation must have the same dimensions. This principle ensures consistency and accuracy.
3. Conversion of Units
   Dimensional analysis simplifies unit conversions, making calculations easier across different measurement systems.

Steps to Perform Dimensional Analysis

1. Identify all variables involved in the problem.
2. Write their dimensions regarding M, L, T, and other fundamental units.
3. Analyze the relationships to confirm consistency or derive new equations.

Applications of Dimensional Analysis

1. Physics
   Dimensional analysis is vital for deriving mechanics, thermodynamics, and electromagnetism equations.
2. Engineering
   Engineers use it to check the validity of models and design systems that adhere to physical laws.
3. Chemistry
   Chemists apply it to understand reaction rates and material properties.
4. Astronomy
   It helps astronomers interpret cosmic distances and velocities accurately.

Advantages of Dimensional Analysis

• Time-Saving: Reduces the need for lengthy computations.
• Error Detection: Quickly identifies inconsistencies in equations.
• Versatility: Applicable across various scientific disciplines.

Limitations of Dimensional Analysis

1. It cannot provide numerical constants.
2. Limited to equations involving physical quantities.
3. Not suitable for complex systems without clear dimensional relationships.

Click Here To See Understanding Bridge Components: A Comprehensive Guide