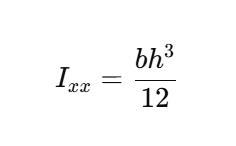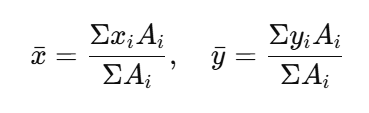Structural engineering involves crucial principles and formulas that ensure the stability and strength of buildings and other structures. Understanding section properties, material properties, and structural analysis is essential for designing safe and efficient support systems. This guide explores key concepts, including centroid calculations, material behavior, and beam analysis formulas.
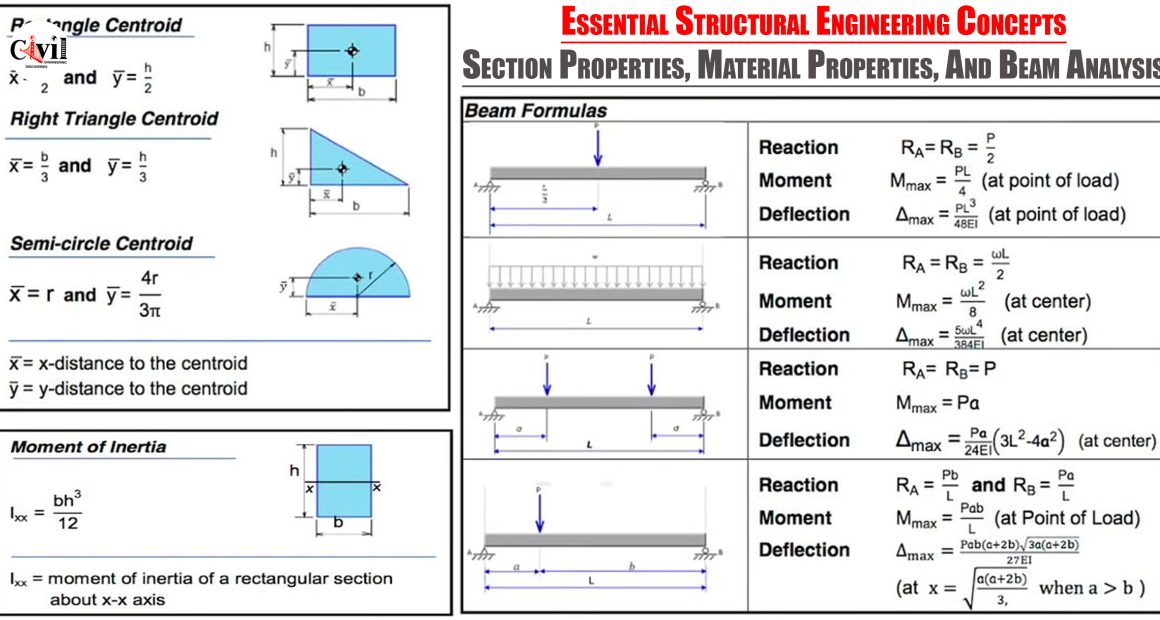
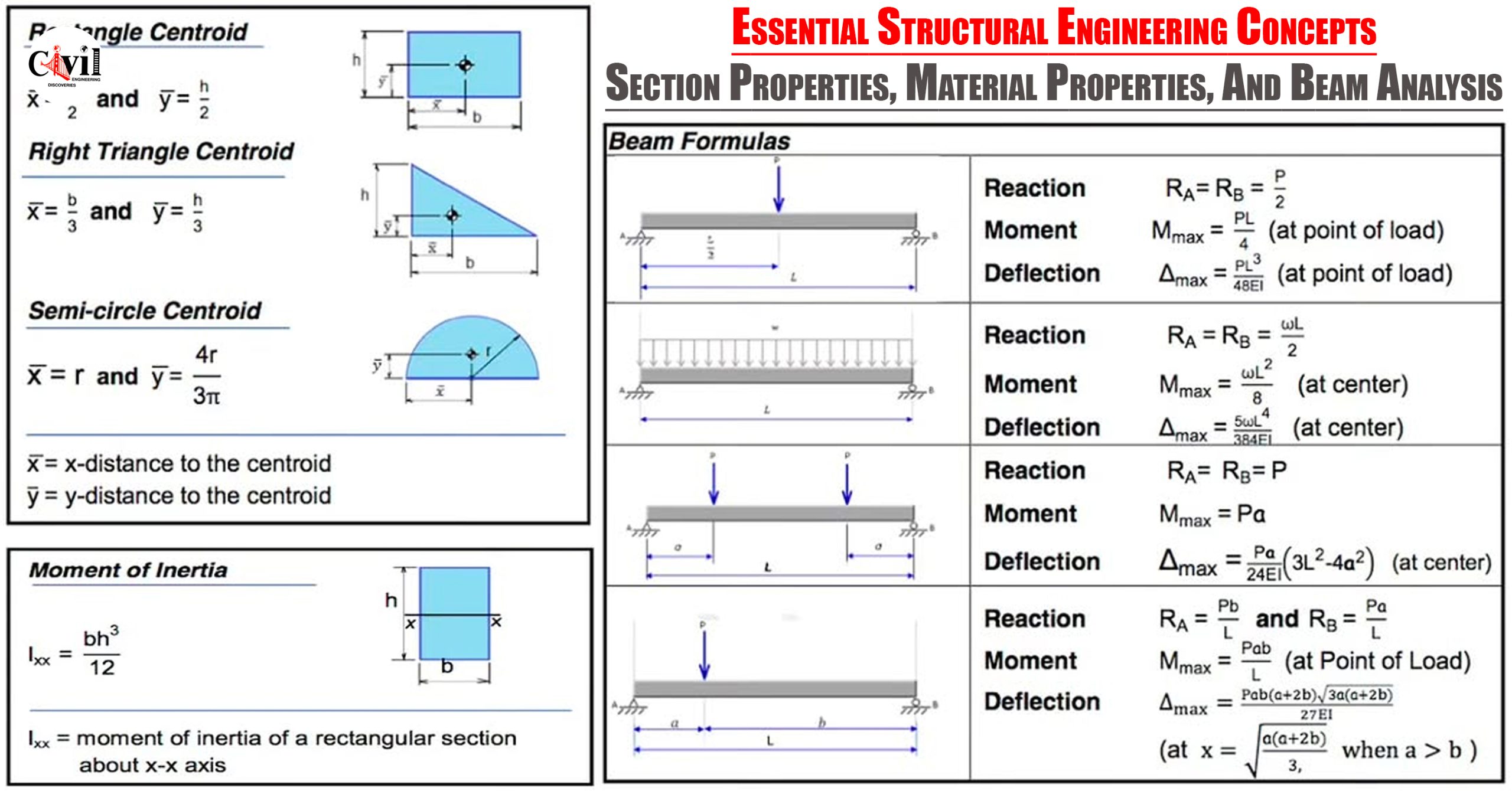
Section Properties: Understanding Centroids and Moment of Inertia
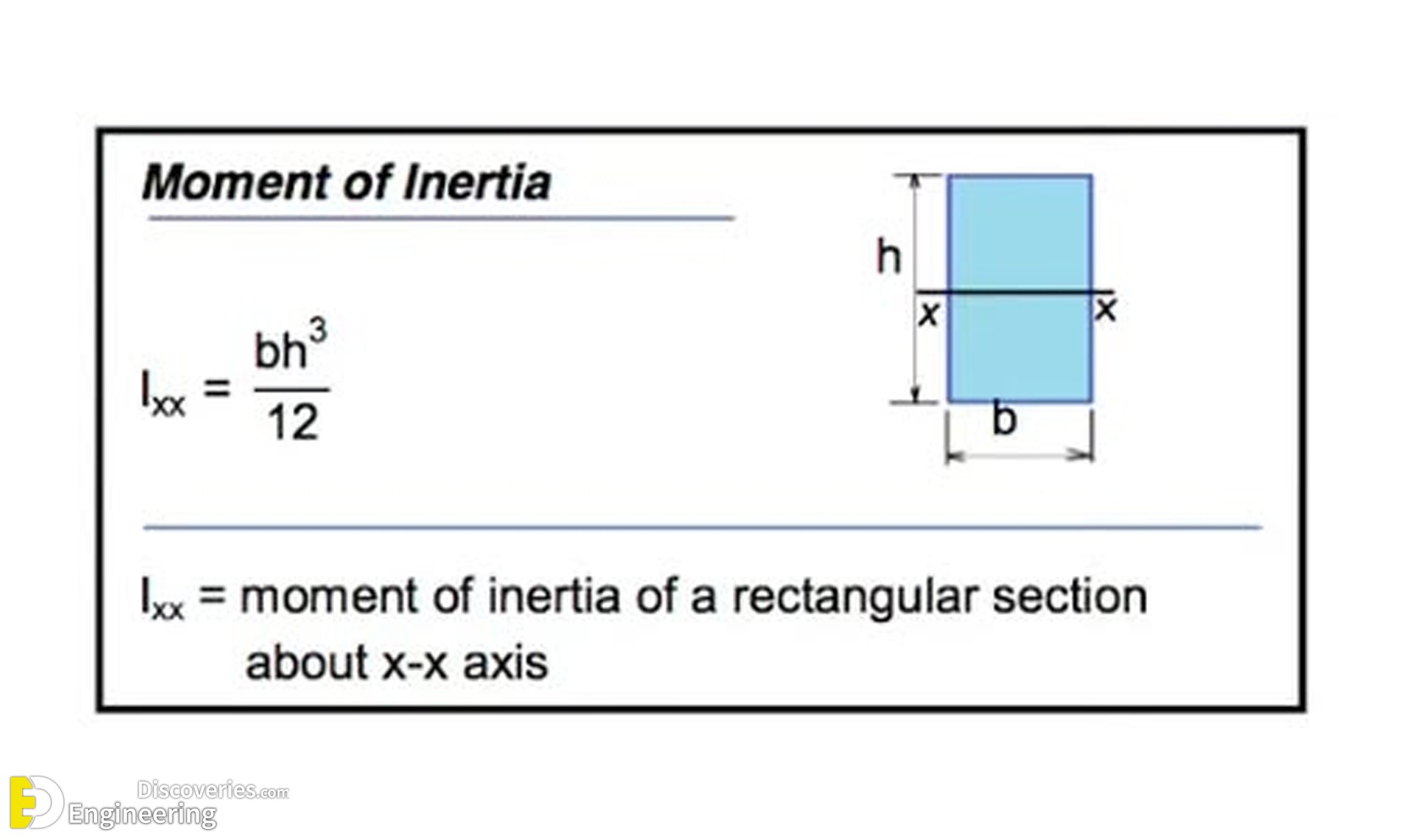
Moment of Inertia (I)
The moment of inertia measures an object’s resistance to bending or rotation about an axis. For a rectangular section, the formula is:
Where:
- b is the width
- h is the height
Centroid Calculations
Centroid locations are crucial for calculating bending stresses and moments. The following are centroid formulas for common shapes:
Material Properties: Stress, Strain, and Modulus of Elasticity
Stress and Strain Relationships
Stress (σ) and strain (ϵ) are fundamental properties that describe how materials respond to forces:
- Stress:
Where:
- F is the applied force
- A is the cross-sectional area
- Strain:
ϵ = δ/L0
Where:
- δ is the change in length
- L0 is the original length
Modulus of Elasticity (E)
The modulus of elasticity defines a material’s ability to deform elastically under stress. It is calculated as:
E = σϵ/E
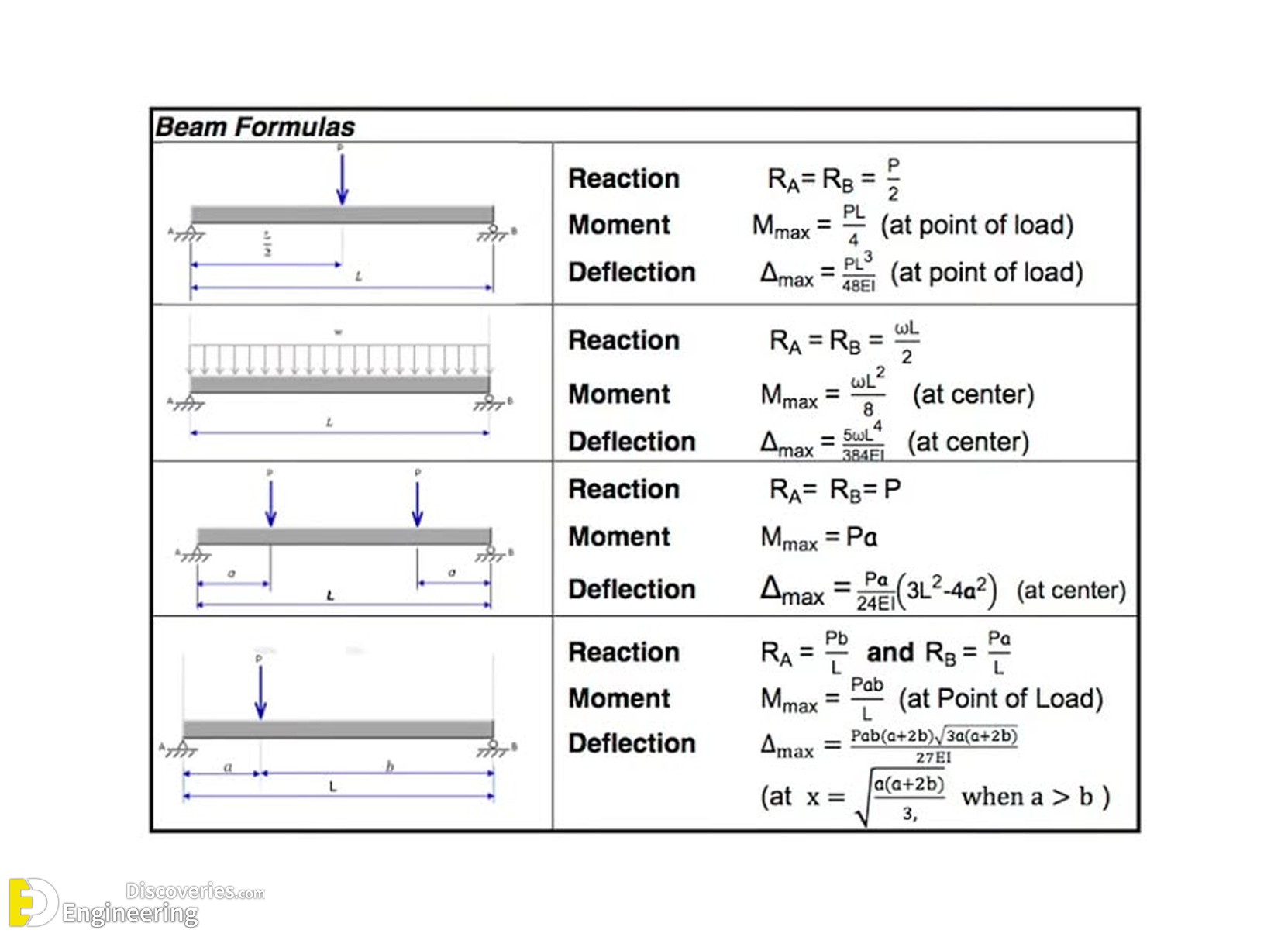
- Reaction at Supports:
RA = RB = 2/P
- Maximum Moment:
Mmax = P/L4
- Deflection:
Δmax = PL^3/48EI
- Reaction at Supports:
RA = RB = wL/2
- Maximum Moment:
- Deflection:
Axial deformation is calculated using the formula:
δ = FL0/AE
Where:
- F is the axial force
- A is the cross-sectional area
- E is the modulus of elasticity
- L_0 is the original length
Truss Analysis Essentials
Truss systems are composed of interconnected members arranged in triangular units. For a stable truss, the equation must be satisfied:
2J = M + R
Where:
- J is the number of joints
- M is the number of members
- R is the number of reaction forces
Click Here To See Understanding Structural Theory – Cheat Sheet Free Download