Understanding the Basics of Bar Spacing
Calculating the centre-to-centre (c/c) distance between reinforcement bars is crucial in structural design. Proper spacing ensures load distribution and structural integrity. Let’s dive into a step-by-step method using a simple example.
Given Data for the Calculation
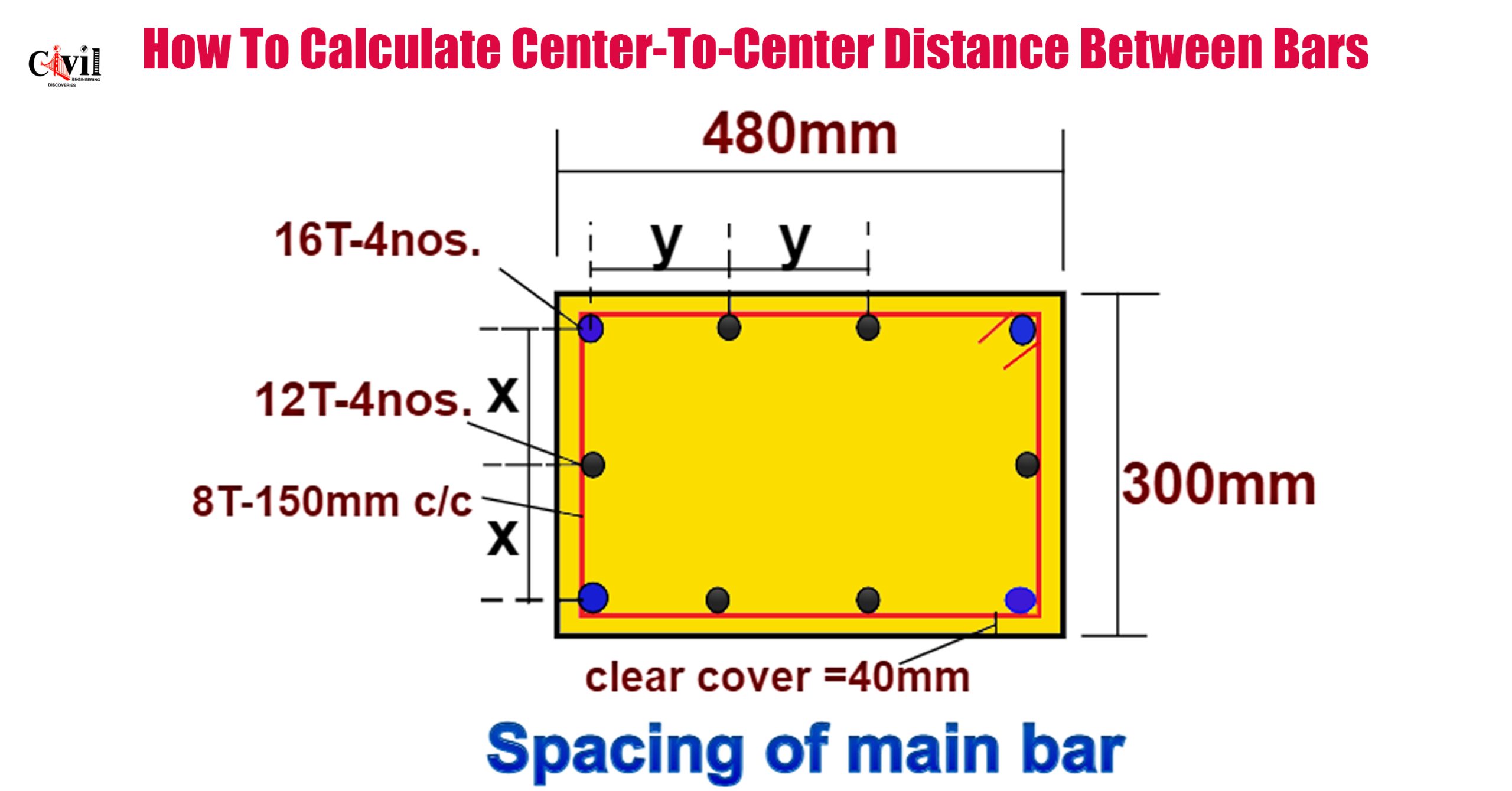
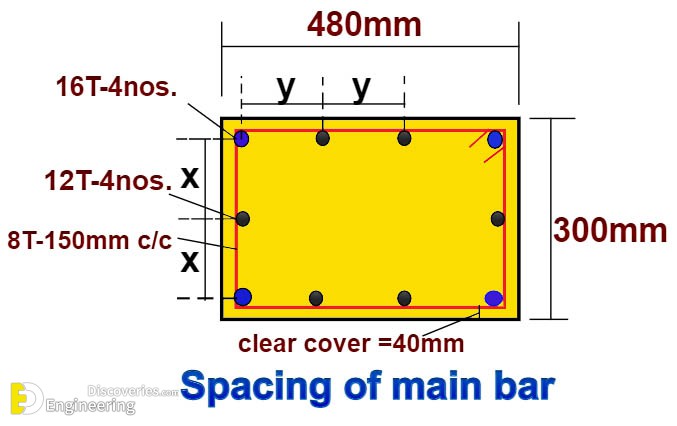
Column Width = 480 mm
Column Depth = 300 mm
Clear Cover = 40 mm
Corner Rebar Diameter = 16 mm
Mid Rebar Diameter = 12 mm
Number of Rebars = 10 nos
Stirrup Bar Diameter = 8 mm
These values form the basis of our calculation.
Step 1: Calculate Centre-to-Centre Distance Along Width (Y-Direction)
First, focus on the width side, commonly called the y-direction.
Formula for Y-Direction Spacing:
y = [Column Width – (2 × Clear Cover) – (2 × Stirrup Bar Diameter) – (2 × ½ × Corner Bar Diameter)] ÷ (Number of Bars Along Width – 1)
Now plug in the values:
y = [480 – (2×40) – (2×8) – (2×½×16)] ÷ (4-1)
Breaking it down:
(2×40) = 80 mm
(2×8) = 16 mm
(2×½×16) = 16 mm
Adding these gives:
80 + 16 + 16 = 112 mm
Subtract from the column width:
480 – 112 = 368 mm
Now divide by (4 – 1) = 3:
368 ÷ 3 = 122.66 mm
Thus, the centre-to-centre distance in the y-direction is 122.66 mm.
Step 2: Calculate Centre-to-Centre Distance Along Depth (X-Direction)
Now, let’s find the spacing along the depth or x-direction.
Formula for X-Direction Spacing:
x = [Column Depth – (2 × Clear Cover) – (2 × Stirrup Bar Diameter) – (2 × ½ × Corner Bar Diameter)] ÷ (Number of Bars Along Depth – 1)
Substituting the values:
x = [300 – (2×40) – (2×8) – (2×½×16)] ÷ (3-1)
Calculation steps:
(2×40) = 80 mm
(2×8) = 16 mm
(2×½×16) = 16 mm
Total = 80 + 16 + 16 = 112 mm
Subtracting from column depth:
300 – 112 = 188 mm
Now divide by (3 – 1) = 2:
188 ÷ 2 = 94 mm
Therefore, the centre-to-centre distance in the x-direction is 94 mm.
Final Result: Spacing in Both Directions
After calculating:
Y-Direction (Width Side) Spacing = 122.66 mm
X-Direction (Depth Side) Spacing = 94 mm
These measurements ensure that reinforcement bars are evenly spaced and structurally sound.
Important Notes for Engineers
This method applies to columns, beams, and slabs.
The spacing remains the same even if you change the rebar diameter.
Always ensure the design follows the relevant structural codes. A correct spacing plan not only increases strength but also improves durability.
Ensure Accurate Bar Placement Every Time
Using this simple calculation, you can confidently design reinforcement layouts. Precision is key in structural engineering, and understanding bar spacing is an essential step toward it. Always double-check your inputs and ensure compliance with project specifications.
Click Here To See How To Calculate The Cutting Length Of A Circular Stirrups Accurately