Ever driven on a curve that felt oddly smooth, like your car naturally followed the bend? That magic is often due to superelevation — a sloped road surface designed to balance forces as vehicles take a curve. It’s not just about comfort; it’s about safety and precision in road engineering.

 Basics of Road Geometry

Before diving into calculations, let’s understand road geometry. Roads aren’t just straight lines — curves are crucial, especially in hilly or urban terrain. These curves come in different shapes, but circular curves are common in design due to their predictability.

Horizontal alignment refers to the plan-view path of a road. Superelevation plays a major role here, helping vehicles maintain stability while navigating these curves.

Superelevation Explained

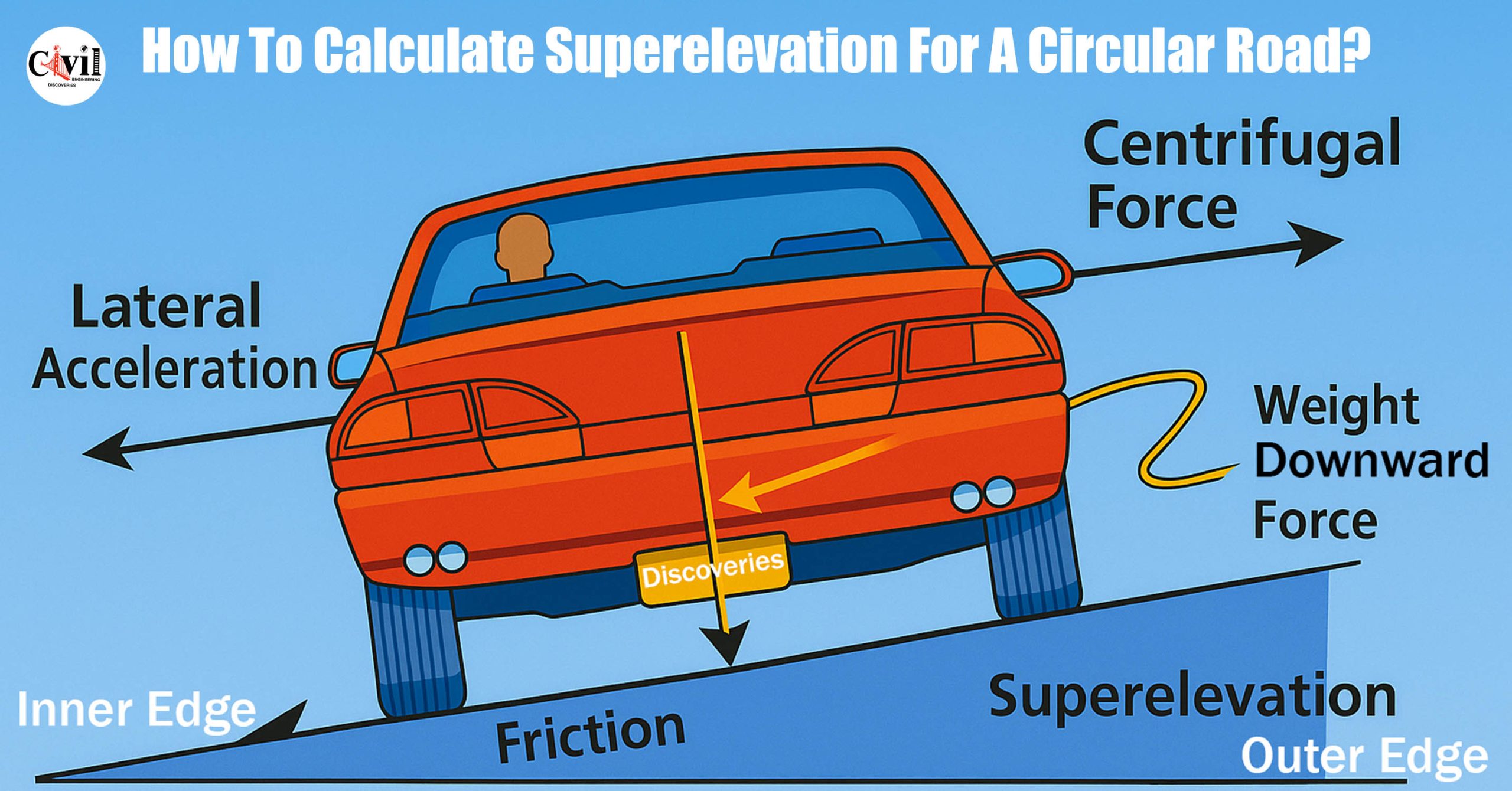
Superelevation is the tilting of the road surface at a curve, raising the outer edge compared to the inner one. This helps counteract the centrifugal force acting on vehicles, keeping them from skidding or overturning.

It’s used:

• On highways and expressways
• In sharp curves
• Where vehicle speeds are high

Factors Affecting Superelevation Design

Designing superelevation isn’t a one-size-fits-all deal. Several factors come into play:

• Design Speed (V): Higher speeds mean more tilt is needed.
• Radius of Curve (R): Sharper curves (smaller R) need greater superelevation.
• Friction Coefficient (f): The grip between tires and the road surface.
• Climate & Terrain: Icy roads or hilly areas may require conservative values.

Superelevation Formula

The general formula to calculate superelevation is:

e + f = V² / (gR)

Where:

• e = superelevation (in decimal)
• f = lateral friction factor
• V = speed of the vehicle (m/s)
• g = acceleration due to gravity (9.81 m/s²)
• R = radius of the curve (m)

If velocity is in KMPH then  e + f = V²/ 127R or cgange the velocity to m/s

Let’s simplify that.

Superelevation Equation Breakdown

To understand better:

• e = the slope (rise/run) of the road
• V = design speed (converted to m/s)
• g = 9.81 m/s² (gravitational constant)
• R = radius of the horizontal curve
• f = side friction factor (usually ranges from 0.10 to 0.15)

You can rearrange the equation to find e if other values are known.

Step-by-Step Calculation Guide

Step 1: Gather Input Data

• Design speed (V) = 90 km/h = 25 m/s
• Radius (R) = 250 m
• f = 0.15

Step 2: Apply Formula

Use:
e + f = V² / (gR)
→ e + 0.15 = (25²) / (9.81 × 250)

Step 3: Solve It

e + 0.15 = 625 / 2452.5
e + 0.15 = 0.2548
e = 0.2548 – 0.15 = 0.1048 (or 10.48%)

Step 4: Check Limits

If the maximum superelevation allowed is 7%, this needs adjustment — either by:

• Reducing design speed
• Increasing radius
• Accepting a higher friction value (if safe)

Design Standards and Limits

Different regions follow different guidelines:

• IRC (India): Max e = 7% in plain terrain
• AASHTO (USA): Max e = 10%
• Minimum e may be zero in urban low-speed areas

Engineers need to stick to these while optimizing the design.

Superelevation Runoff

This is the length of road needed to transition from normal camber (flat) to full superelevation. Runoff depends on:

• Road type
• Speed
• Curve sharpness

Proper runoff ensures driver comfort and avoids sudden jolts or wheelspin.

Real-Life Example

Problem:

Design superelevation for a curve with:

• Radius = 300 m
• Speed = 80 km/h
• Friction = 0.14

Solution:

Speed in m/s = 80 × 1000 / 3600 = 22.22 m/s
e + 0.14 = (22.22²) / (9.81 × 300)
e + 0.14 = 0.168
e = 0.028 or 2.8%

2.8%< 7%, hence safe.

✅ Within limits – good design!

Superelevation vs Banking

People often use these interchangeably. They’re similar, but:

• Superelevation is engineered into roads
• Banking often refers to curves in racing tracks or natural slopes

In essence, superelevation is calculated and controlled.

Practical Considerations

• Urban roads often avoid full superelevation due to pedestrians and drainage.
• Rural highways utilize full design values for safety at higher speeds.
• Rain and snow reduce friction, so lower superelevation may be chosen with broader curves.

Tools Used for Superelevation Design

Modern design uses both manual and digital tools:

• AutoCAD Civil 3D
• MX Road
• IRC/AASHTO design manuals
• Total stations and survey tools

These help ensure accuracy and compliance with standards.

Common Mistakes to Avoid

• Overestimating speed without real traffic data
• Choosing unrealistic friction values
• Ignoring transition length/runoff
• Not checking against regional codes

Benefits of Proper Superelevation

• Improved vehicle handling
• Reduced skidding and overturning risk
• Enhanced ride comfort
• Better longevity for road surface

Click Here To See How To Derive Formula For Super-Elevation Of Bending Road