Understanding Tensional Forces in Supporting Wires
Tensional forces often act through wires and ropes in mechanical systems. When three forces act at a point and are in equilibrium, Lami’s Theorem helps calculate the unknown forces.
What is Lami’s Theorem?
Lami’s Theorem states that if three coplanar forces keep a body in equilibrium, each force is proportional to the sine of the angle between the other two forces. The formula is:
T₁ / sin(θ₁) = T₂ / sin(θ₂) = T₃ / sin(θ₃)
This relation is essential when solving for tensions in wires holding up a load.
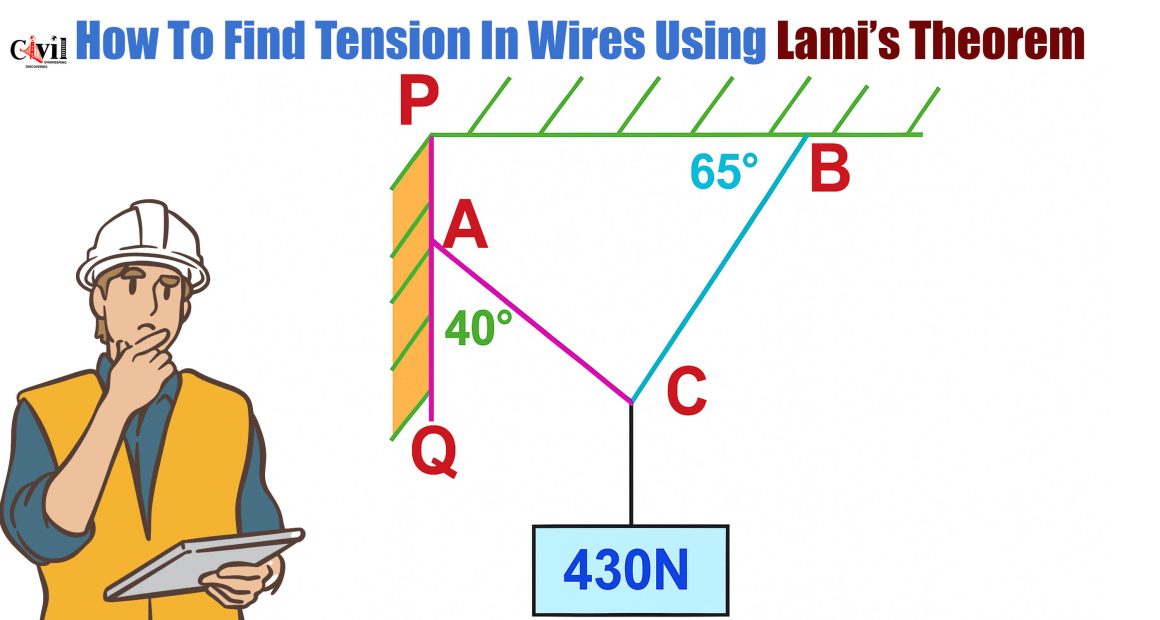
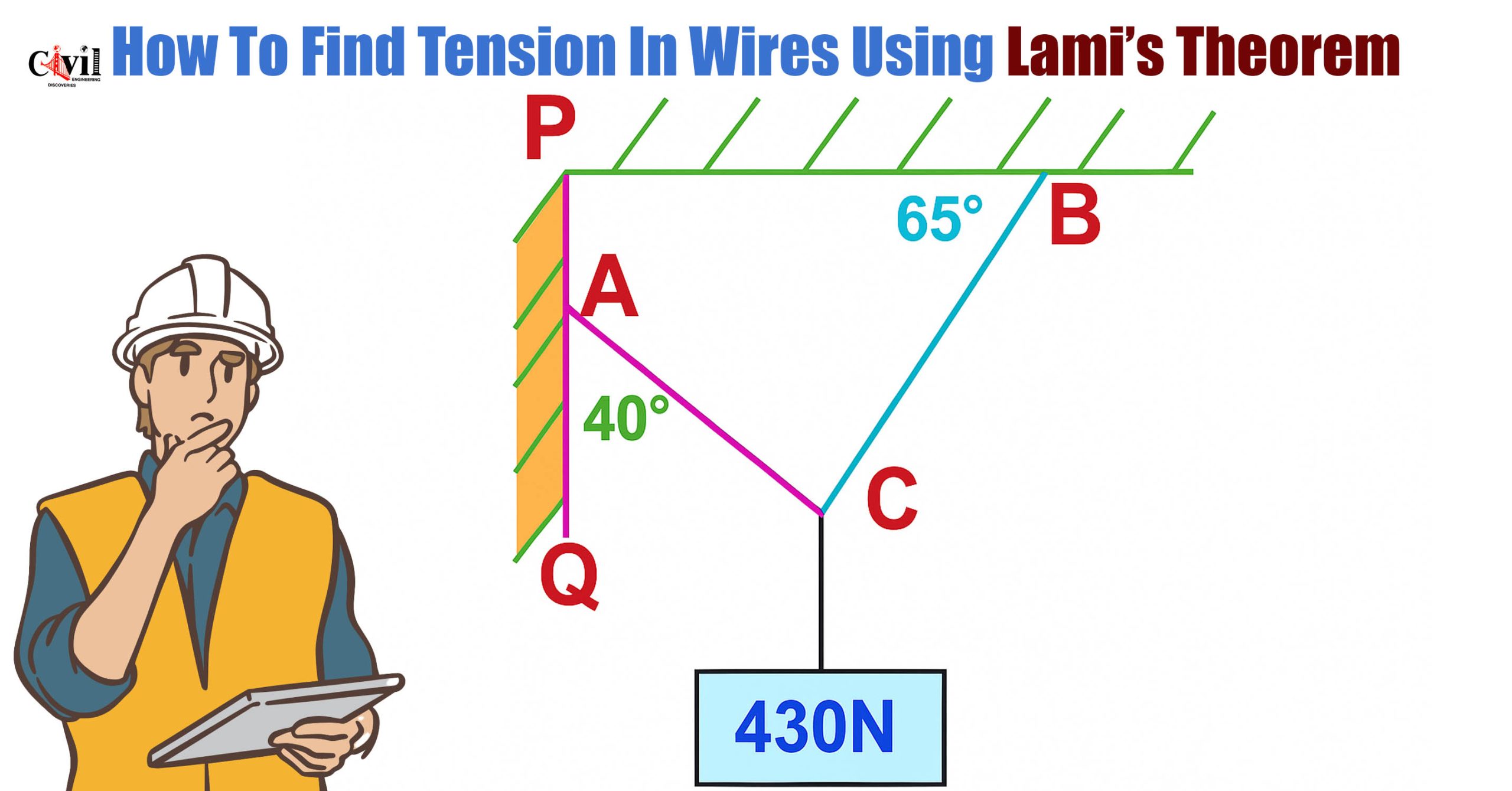
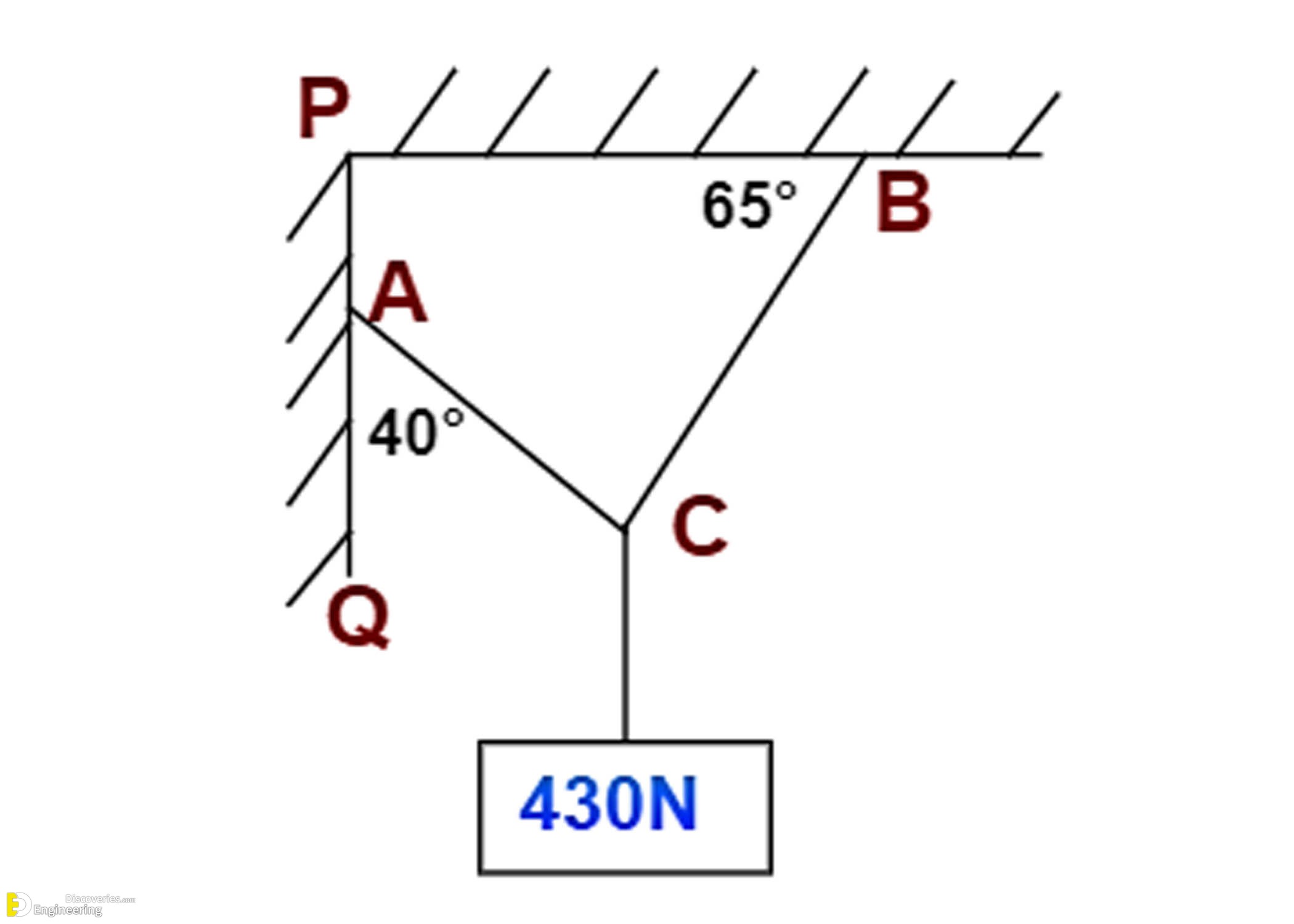
Example Problem: Find Tensions in Wires AC and BC
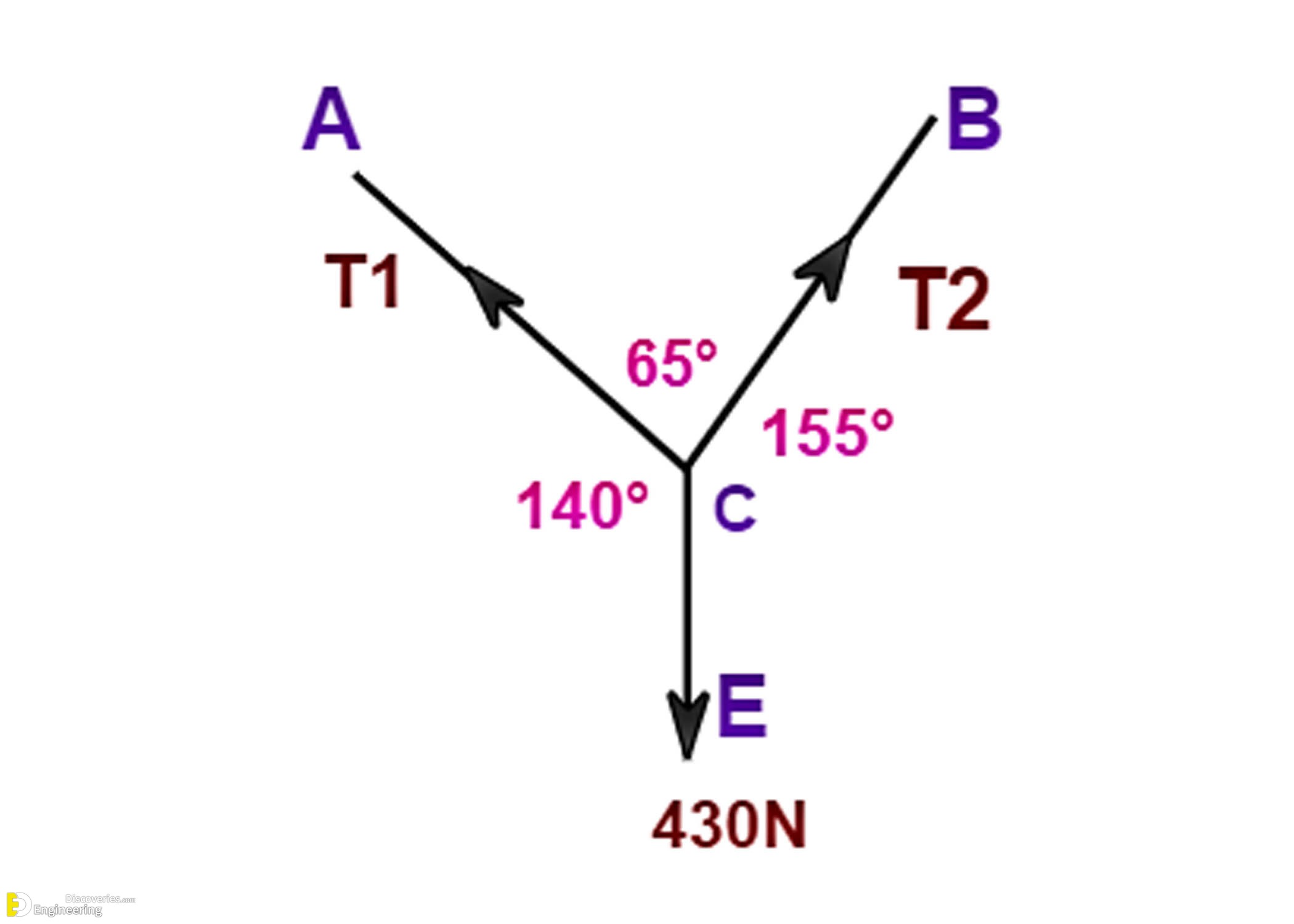
Let’s calculate the tensile forces in AC and BC wires that support a 430N vertical load.
Step 1: Geometry and Angles
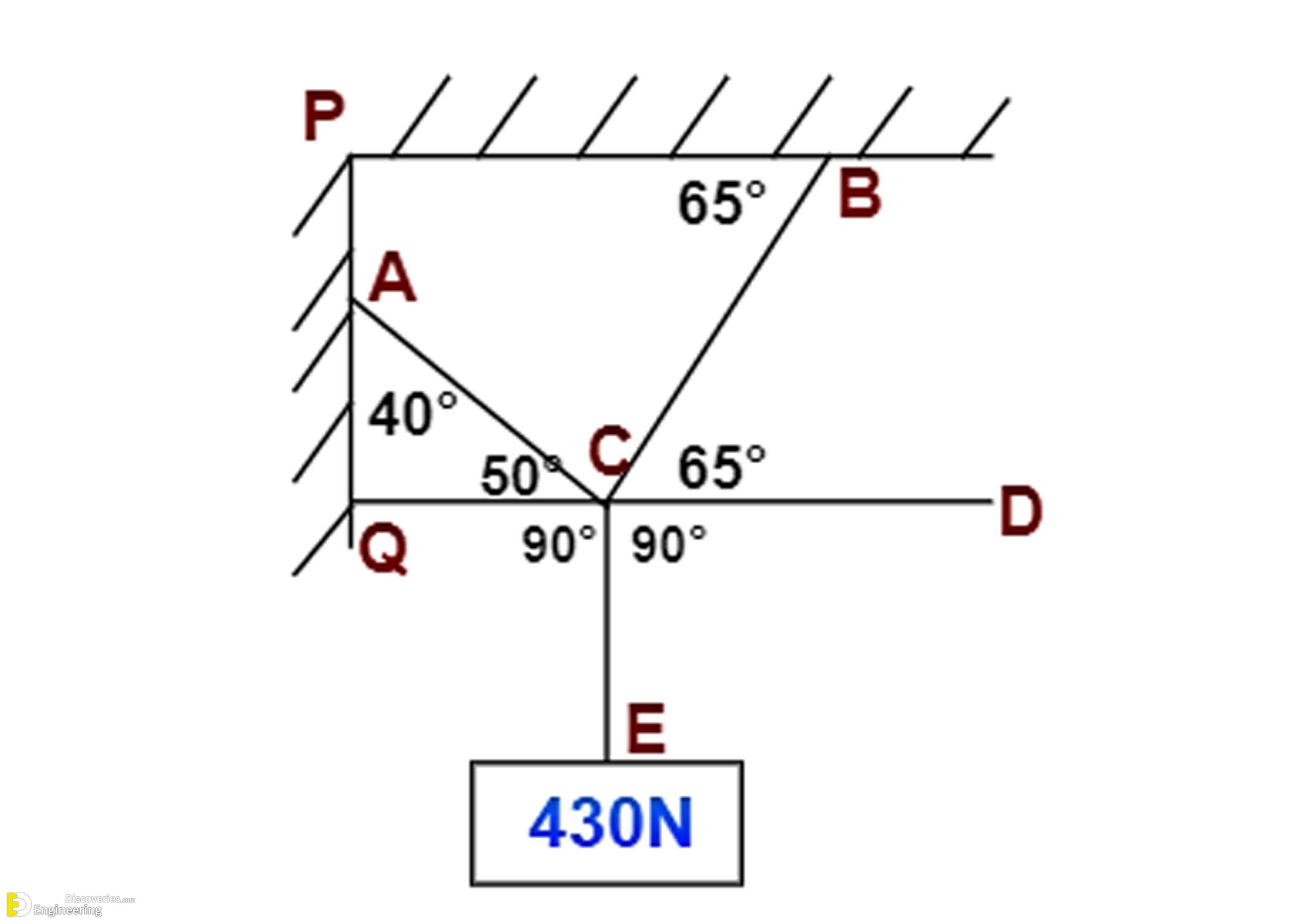
Draw a line QD parallel to support PB through the point C. Given:
∠B = 65°, so ∠BCD = 65° (alternate angles rule)
Line QD is perpendicular to QP, so ∠Q = 90°
Now, in triangle AQC:
∠A = 40°
∠Q = 90°
So,
∠C = 180° – (90° + 40°) = 50°
Step 2: Free-Body Diagram Angles
The vertical force acts downward, so:
∠QCE = ∠DCE = 90°
Calculate:
∠ACE = ∠ACQ + ∠QCE = 50° + 90° = 140°
∠BCE = ∠BCD + ∠DCE = 65° + 90° = 155°
Now, use the angle sum around point C:
∠ACB = 360° – (∠ACE + ∠BCE)
∠ACB = 360° – (140° + 155°) = 65°
Step 3: Applying Lami’s Theorem
Now apply Lami’s Theorem to solve for T₁ (AC) and T₂ (BC):
T₁ / sin(155°) = T₂ / sin(140°) = 430N / sin(65°)
Step 4: Calculate Tension in Wire AC (T₁)
T₁ = [430N ÷ sin(65°)] × sin(155°)
T₁ = [430 ÷ 0.906] × 0.422
T₁ = 474.61 × 0.422 = 200.29N
Step 5: Calculate Tension in Wire BC (T₂)
T₂ = [430N ÷ sin(65°)] × sin(140°)
T₂ = [430 ÷ 0.906] × 0.643
T₂ = 474.61 × 0.643 = 305.08N
Final Result: Tension Forces
Tension in wire AC = 200.29 N
Tension in wire BC = 305.08 N