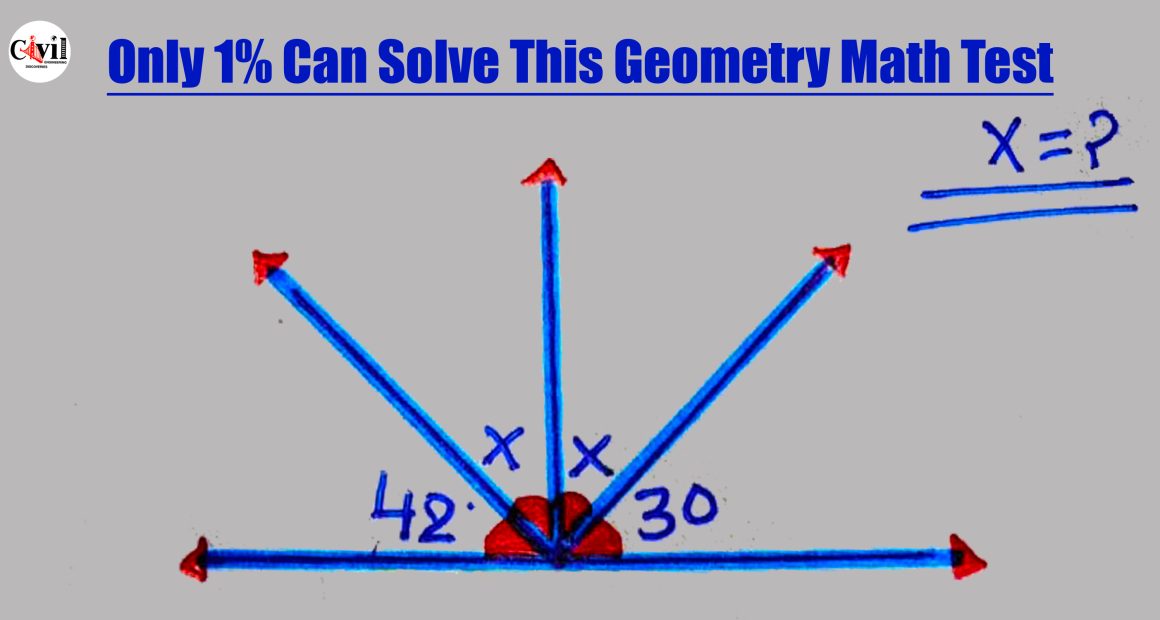
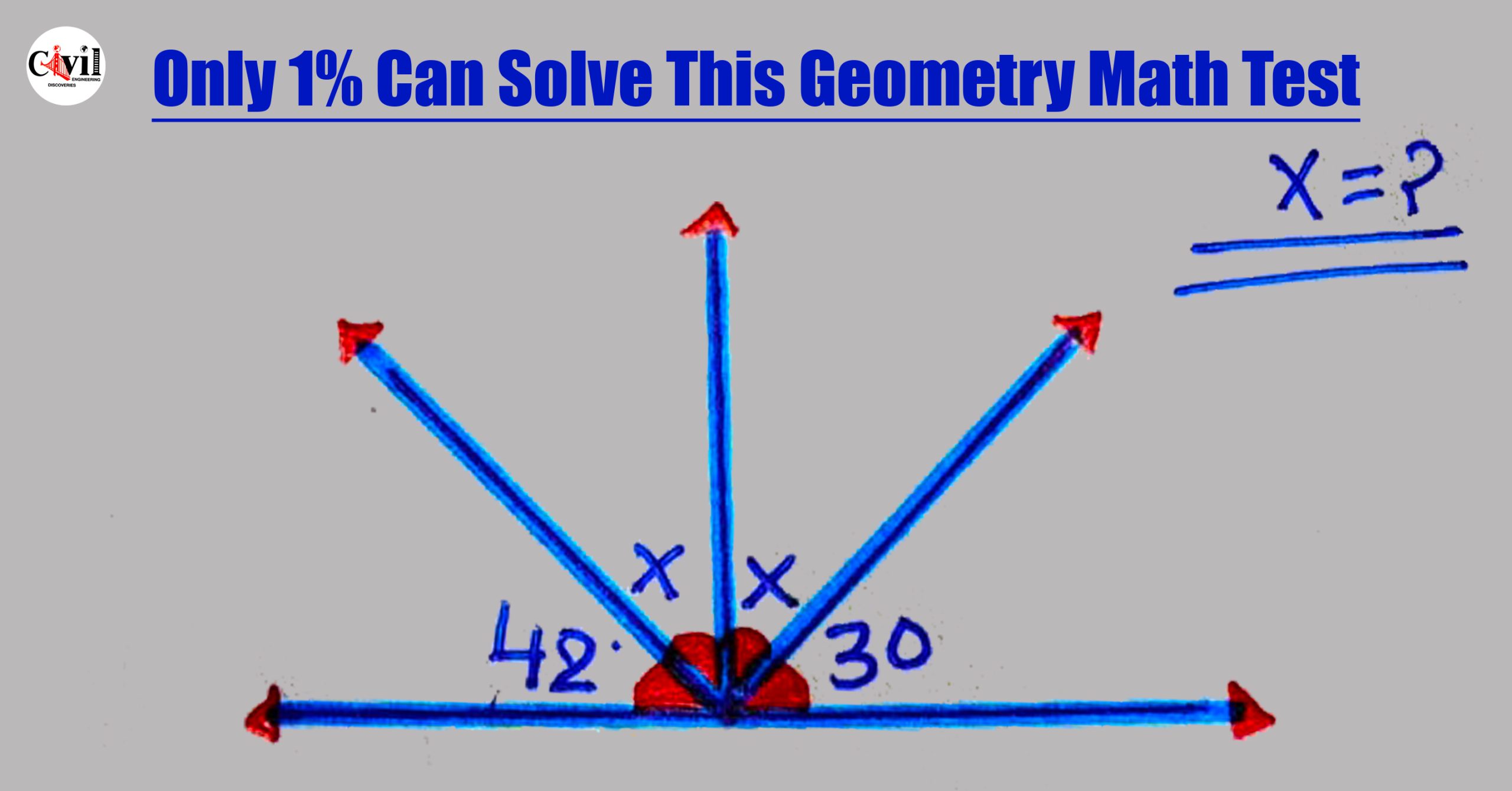
Let’s analyze the given diagram and solve for angle x.
Step 1: Understanding the Given Information
The diagram shows multiple angles around a straight line.
A straight line forms a total of 180°.
The given angles are 42° and 30°.
The two unknown angles are marked as x.
Step 2: Setting Up the Equation
Since all the angles on a straight line sum to 180°, we can write the equation as:
42° + x + x + 30° = 180°
42° + 2x + 30° = 180°
72° + 2x = 180°
2x = 180° – 72°
2x = 108°
x = 108°/2
x = 54°
Thus, the missing angle is 54°.
The Importance of Angles in Geometry
Types of Angles
- Acute Angles: Less than 90°
- Right Angles: Exactly 90°
- Obtuse Angles: Greater than 90° but less than 180°
- Straight Angles: Exactly 180°
- Reflex Angles: Greater than 180° but less than 360°
Understanding these angles is crucial for solving geometric problems efficiently.
Angles on a Straight Line
A fundamental rule in geometry states that the sum of angles on a straight line is always 180°. This principle helps in solving many mathematical problems, including the example above.
Angles in a Triangle
The sum of the interior angles of a triangle is always 180°. This rule is useful for finding missing angles when two angles are known.
Angles in Parallel Lines
When two parallel lines are intersected by a transversal, several angle relationships arise:
- Corresponding angles are equal.
- Alternate interior angles are equal.
- Co-interior angles sum to 180°.
Click Here To See 97% FAIL This Puzzle! 3-4=8 Can You Fix Mind-Blowing Puzzle In 1 Move!
