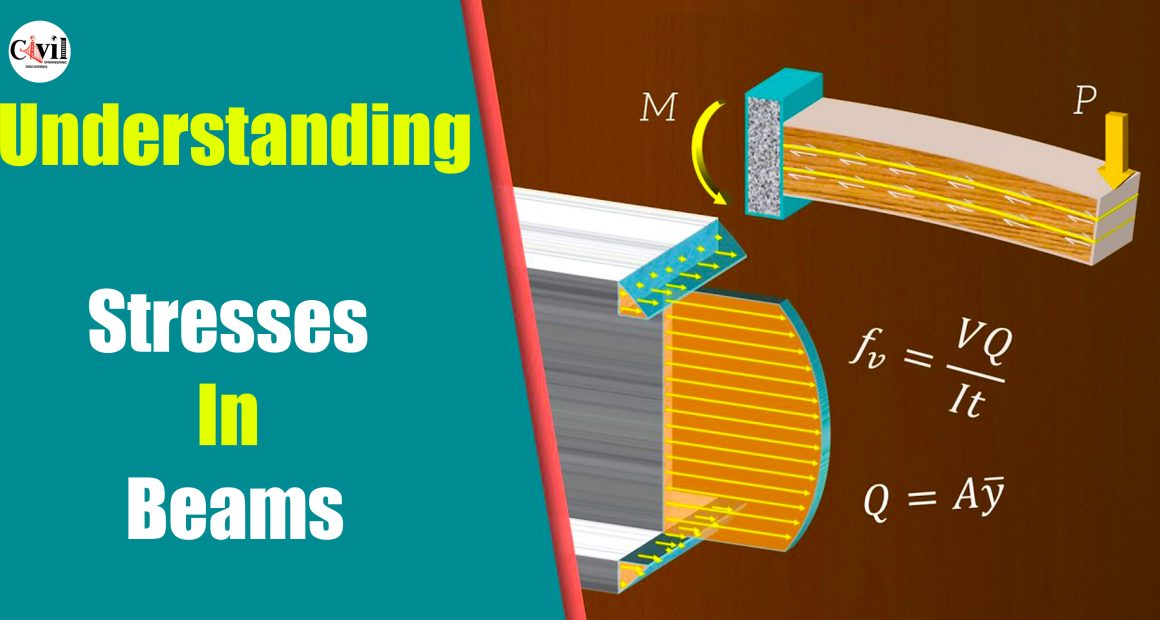
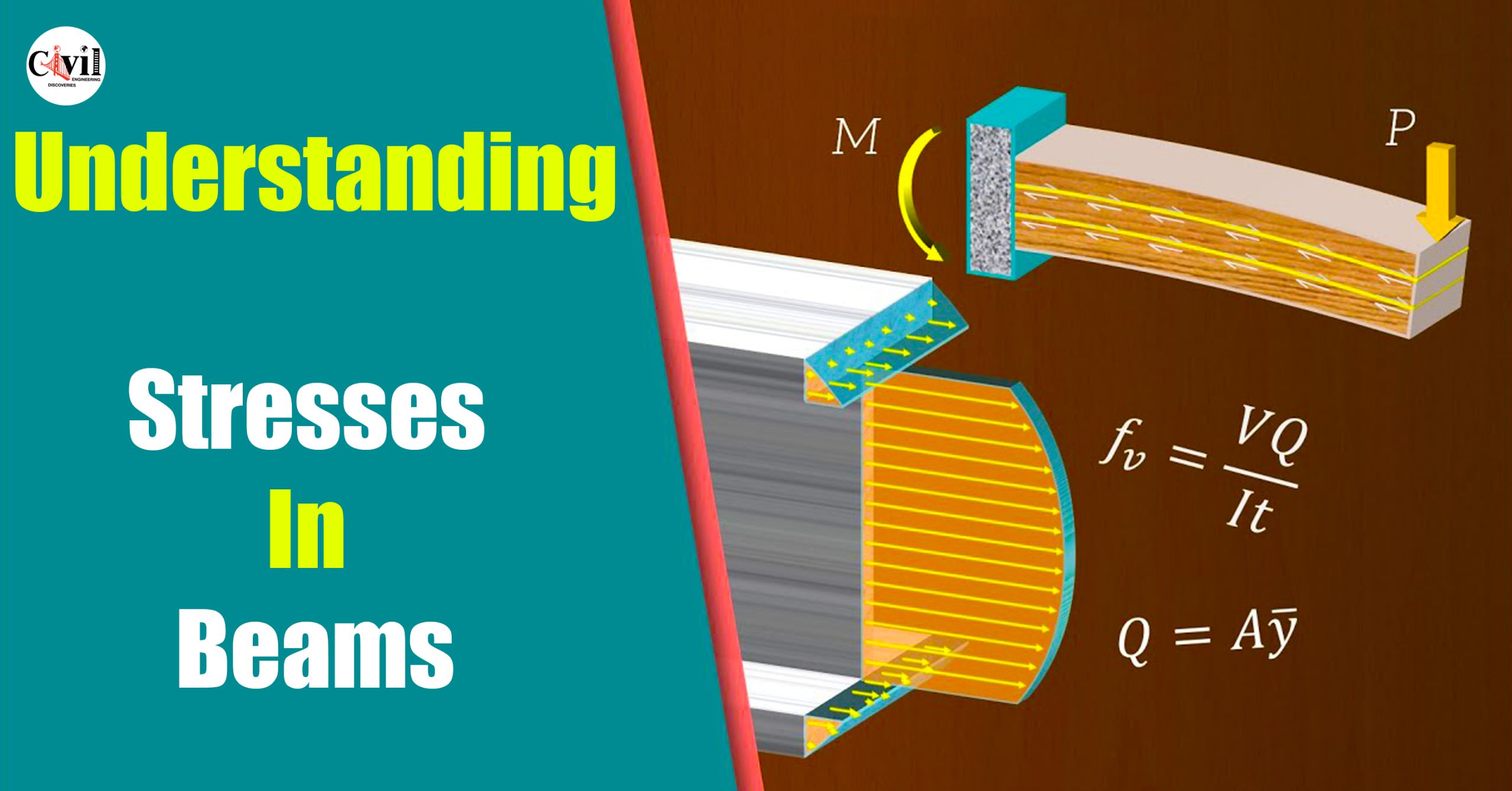
In this video, we explore bending and shear stresses in beams. A bending moment is the resultant of bending stresses, which are normal stresses acting perpendicular to the beam cross-section. We can easily derive an equation for these bending stresses by observing how a beam deforms in a case of pure bending. This equation is known as the flexure formula.

Next, we look at shear stresses, which act parallel to the beam cross-section and can be represented by a shear force. These vertical shear stresses can cause horizontal shear failure in beams because they result in complementary horizontal shear stresses, which develop to maintain equilibrium.

Finally, we look at how we can apply the shear stress equation to thin-walled open sections like the I beam, and how shear stress appears to “flow” through the cross-section.

Errata:

• The moment shown at 07:38 is drawn in the wrong direction.
• The shear stress profile shown at 11:41 is incorrect – the correct profile has the maximum shear stress at the edges of the cross-section and the minimum shear stress at the center.