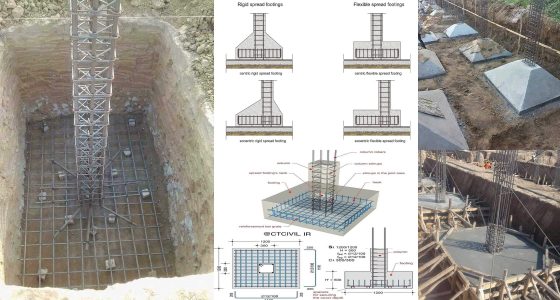
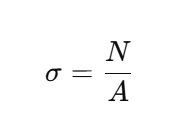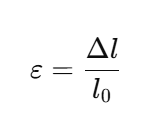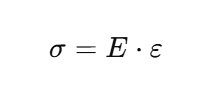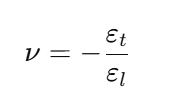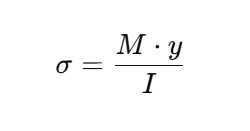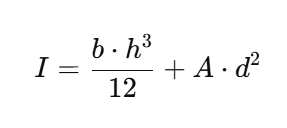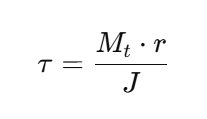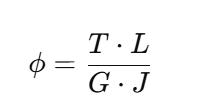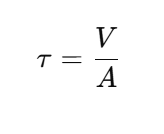Understanding the mechanics of materials is essential for engineers, architects, and anyone involved in the analysis and design of structures. This discipline, also known as the strength of materials, examines how different materials deform under various types of forces, including tension, compression, bending, shear, and torsion. In this guide, we explore critical formulas, concepts, and applications that define this foundational field.
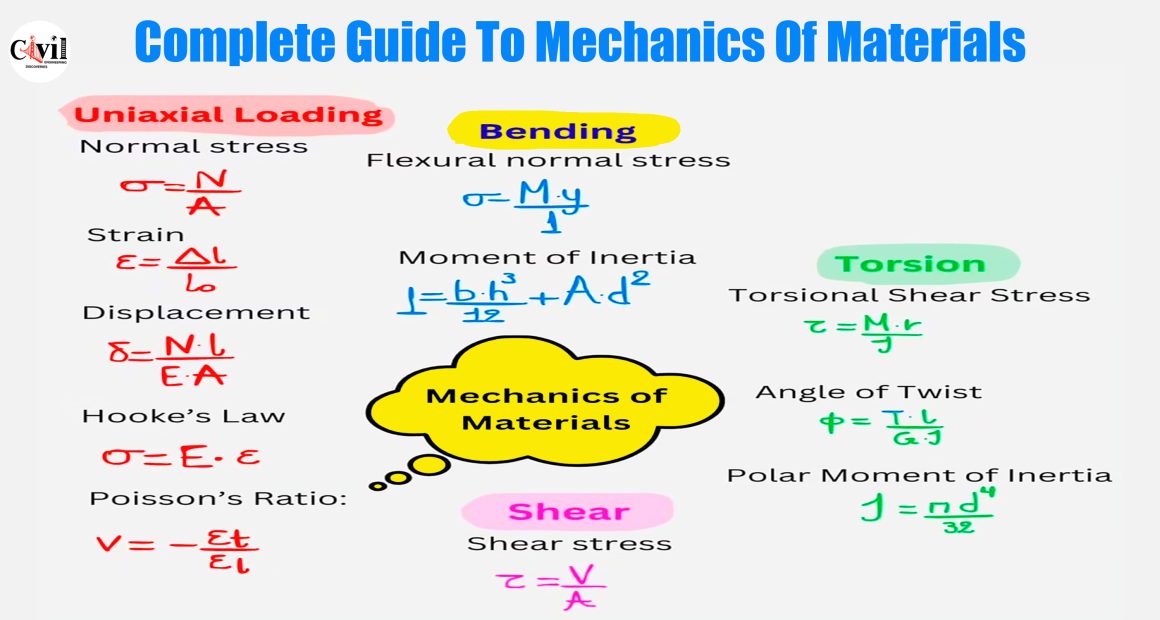
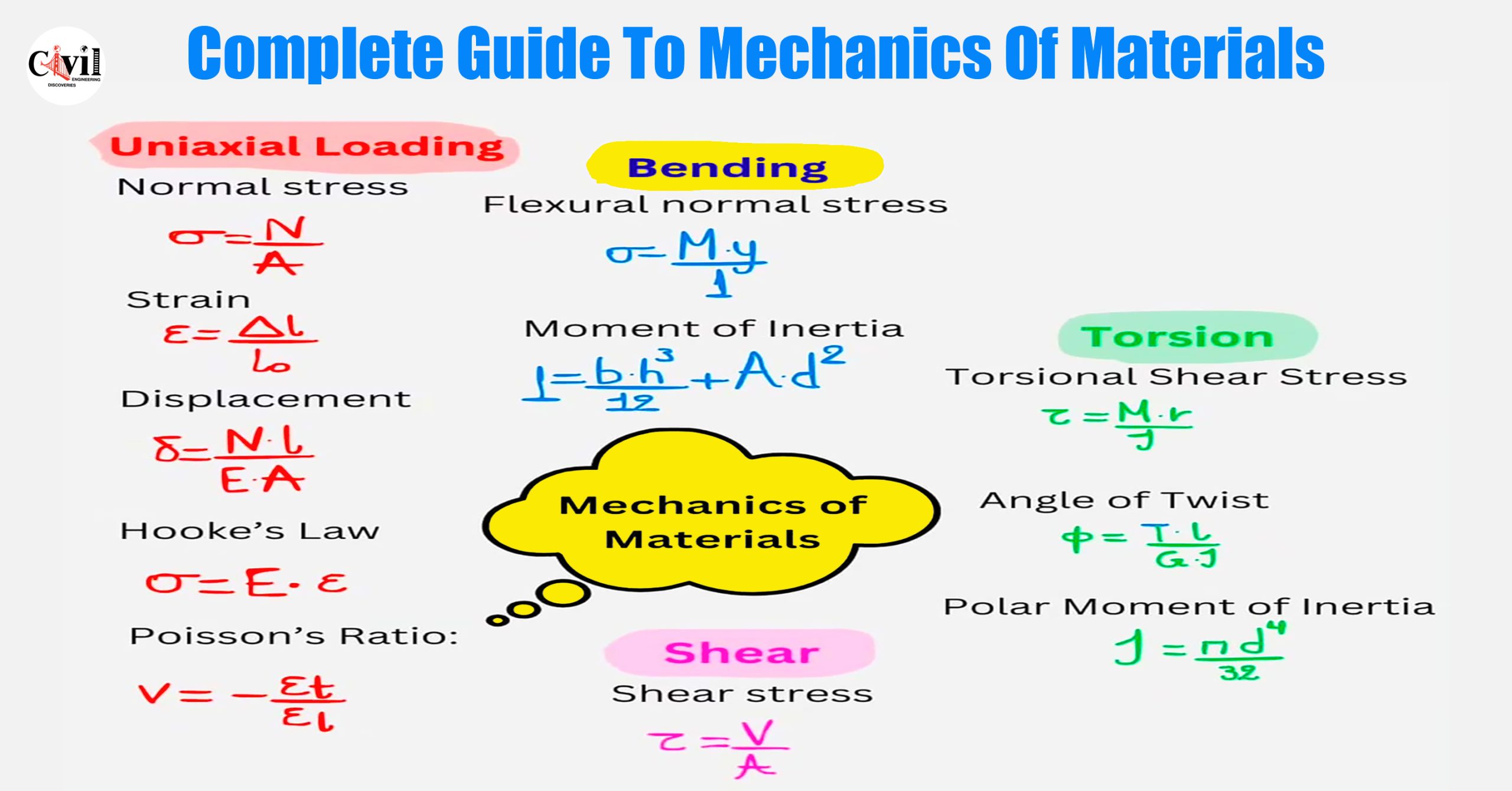
Uniaxial Loading: Understanding Normal Stress and Strain
🔴 Normal Stress (σ)
Formula:
Where:
N is the axial force
A is the cross-sectional area
Normal stress is induced when a force acts perpendicular to the surface of a material. It plays a pivotal role in determining whether a component will fail under tension or compression.
🔴 Strain (ε)
Formula:
Strain represents the deformation per unit length caused by an applied stress. It is a dimensionless quantity that gives engineers insight into material elongation.
🔴 Displacement (δ)
Formula:
This formula calculates how much a member will elongate or compress under axial loading.
🔴 Hooke’s Law
Formula:
Hooke’s Law describes the linear relationship between stress and strain for elastic materials.
🔴 Poisson’s Ratio (ν)
Formula:
Poisson’s ratio defines how materials laterally contract when stretched or expand when compressed.
Bending: Flexural Stress and Moment of Inertia
🟣 Flexural Normal Stress
Formula:
Where:
M is the bending moment
y is the distance from the neutral axis
I is the moment of inertia
This relationship governs stress distribution across a beam subjected to bending.
🟣 Moment of Inertia (I)
Formula:
This is a geometric property of a cross-section that influences a member’s resistance to bending and deflection.
Torsion: Shear Stress and Angle of Twist
🟢 Torsional Shear Stress (τ)
Formula:
Where:
Mt is the torque
r is the radial distance
J is the polar moment of inertia
Torsional shear stress is critical when designing shafts and rotating members.
🟢 Angle of Twist (ϕ)
Formula:
The angular deformation due to torque is a function of the shaft’s geometry and the material’s shear modulus G.
🟢 Polar Moment of Inertia (J)
Formula:
This defines a circular shaft’s resistance to torsional deformation.
Shear: Internal Forces Acting Parallel
Shear Stress
Formula:
Where:
is the shear force
A is the area over which the force acts
This type of stress is especially important in bolted joints, riveted connections, and structural beams.
Applications of Mechanics of Materials in Engineering
Understanding these principles allows engineers to design safer, more efficient structures. Here are some real-world applications:
Structural Engineering
Structural beams in bridges and buildings are designed using principles of bending and shear to withstand loads safely.
Mechanical Engineering
In automotive engineering, torsional stress and angle of twist help design drive shafts and steering systems.
Aerospace Engineering
Aircraft components are subjected to complex loading combinations. Mechanics of materials helps in fatigue analysis and lightweight design.
Civil Engineering
Long-span buildings and towers are analyzed for displacement and stress using the core principles of mechanics of materials.
Advanced Topics for Deeper Mastery
Fatigue and Creep
These time-dependent behaviors involve the response of materials under cyclic or long-term loading. Mastering fatigue life calculations ensures the longevity of structures.
Stress Concentration
Areas with abrupt geometry changes (like holes and notches) experience higher stress. Understanding this concept helps minimize failure.
Composite Materials
Modern engineering uses layered or fiber-reinforced composites that respond differently under load. Mechanics of materials adapts to analyze such materials.
Why Mastering These Equations Matters
Each formula included in mechanics of materials is essential for a specific type of structural analysis. Together, they form a comprehensive toolkit that enables:
Accurate stress analysis
Failure prediction
Optimal material usage
Cost-efficient design
Compliance with safety standards
Click Here To See 4 Important Rules When Designing A Concrete Torsion-Exposed Beam