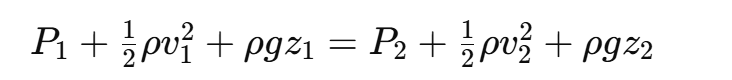Introduction
Fluid dynamics plays a crucial role in many scientific and engineering fields. One of the most fundamental principles governing fluid behavior is Bernoulli’s Equation. This equation helps explain how fluids move through different points in a system, influencing everything from aviation to plumbing. In this article, we explore the volume flow rate, incompressible liquids, continuity equation, and the work-energy theorem.
What is Bernoulli’s Equation?
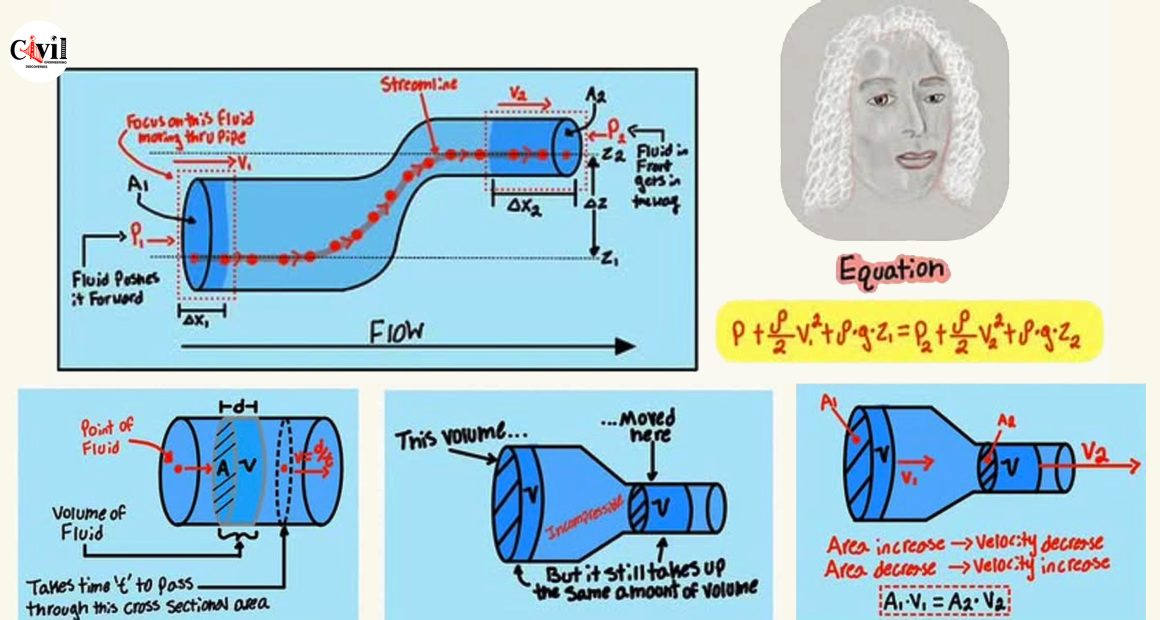
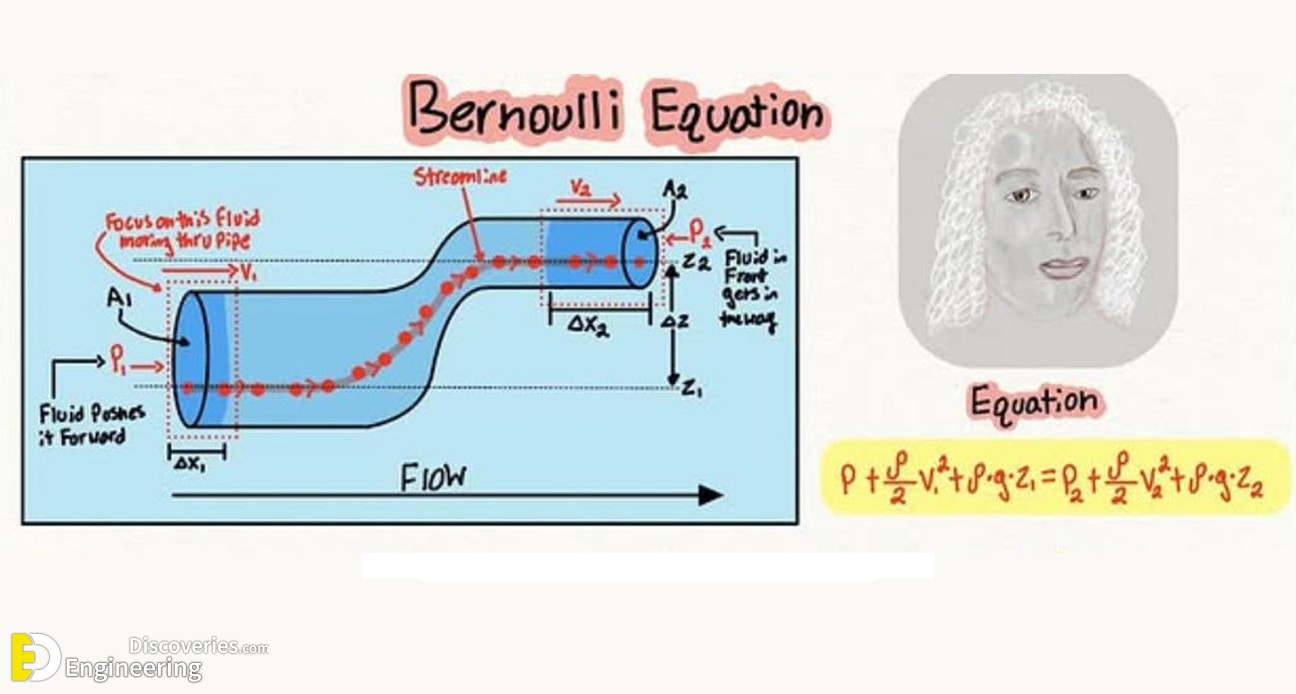
Bernoulli’s equation is a mathematical representation of the conservation of energy in a flowing fluid. It states that the total mechanical energy of the fluid remains constant along a streamline. The equation is expressed as:
P + ½ρV² + ρgz = Constant
- P = Pressure energy per unit volume
- = Fluid density
- v = Fluid velocity
- g = Acceleration due to gravity
- z = Height above a reference point
This equation explains why fluids move faster through narrow passages and slower through wider ones.
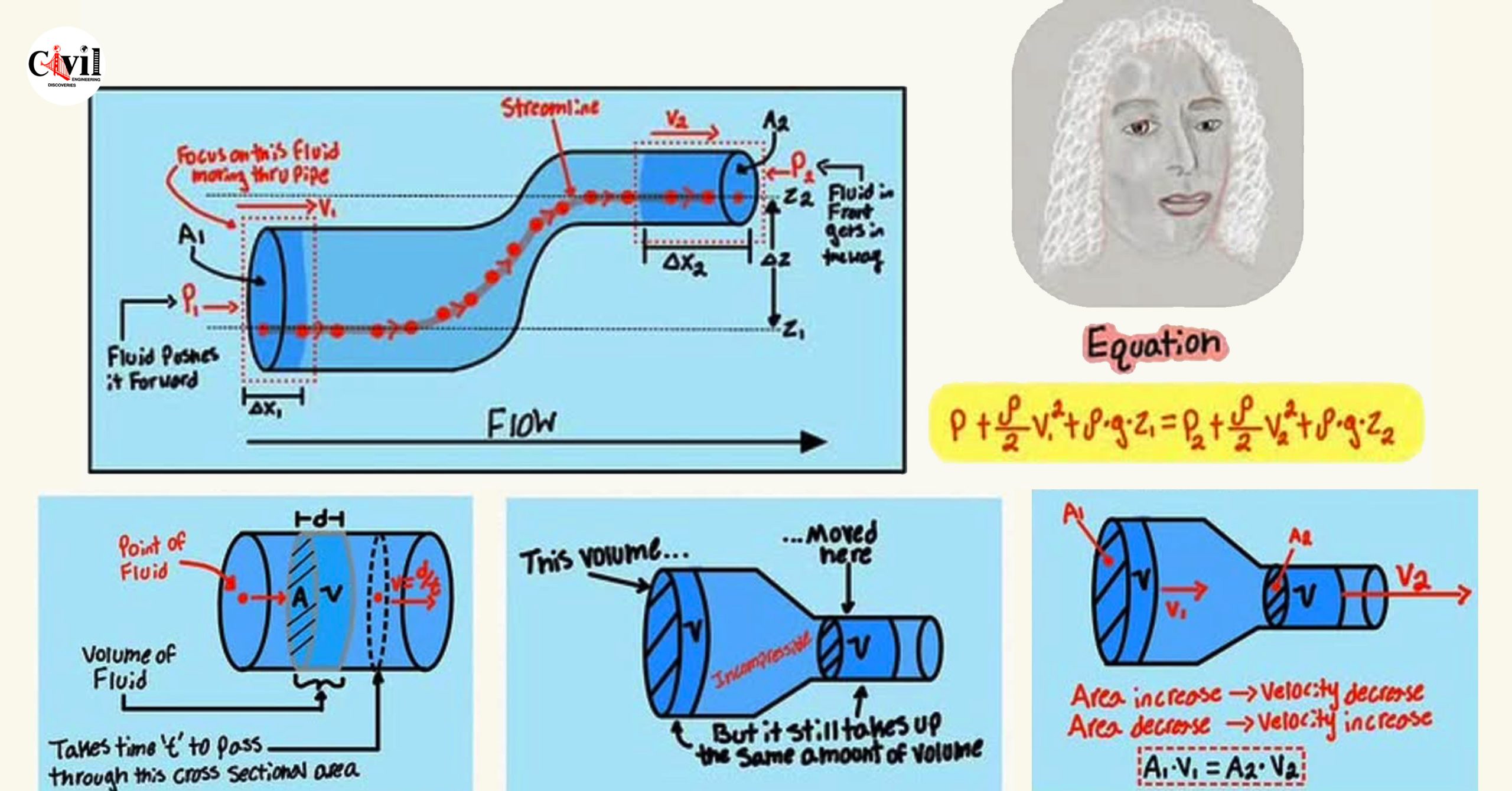
Volume Flow Rate: The Measure of Fluid Movement
Volume flow rate is the amount of fluid passing through a given cross-sectional area per unit of time. It is defined as:
Q = A × V
Where:
- Q = Volume flow rate (m³/s)
- A = Cross-sectional area (m²)
- v = Velocity of the fluid (m/s)
This principle is essential for understanding how fluids behave in pipes, rivers, and even blood vessels.
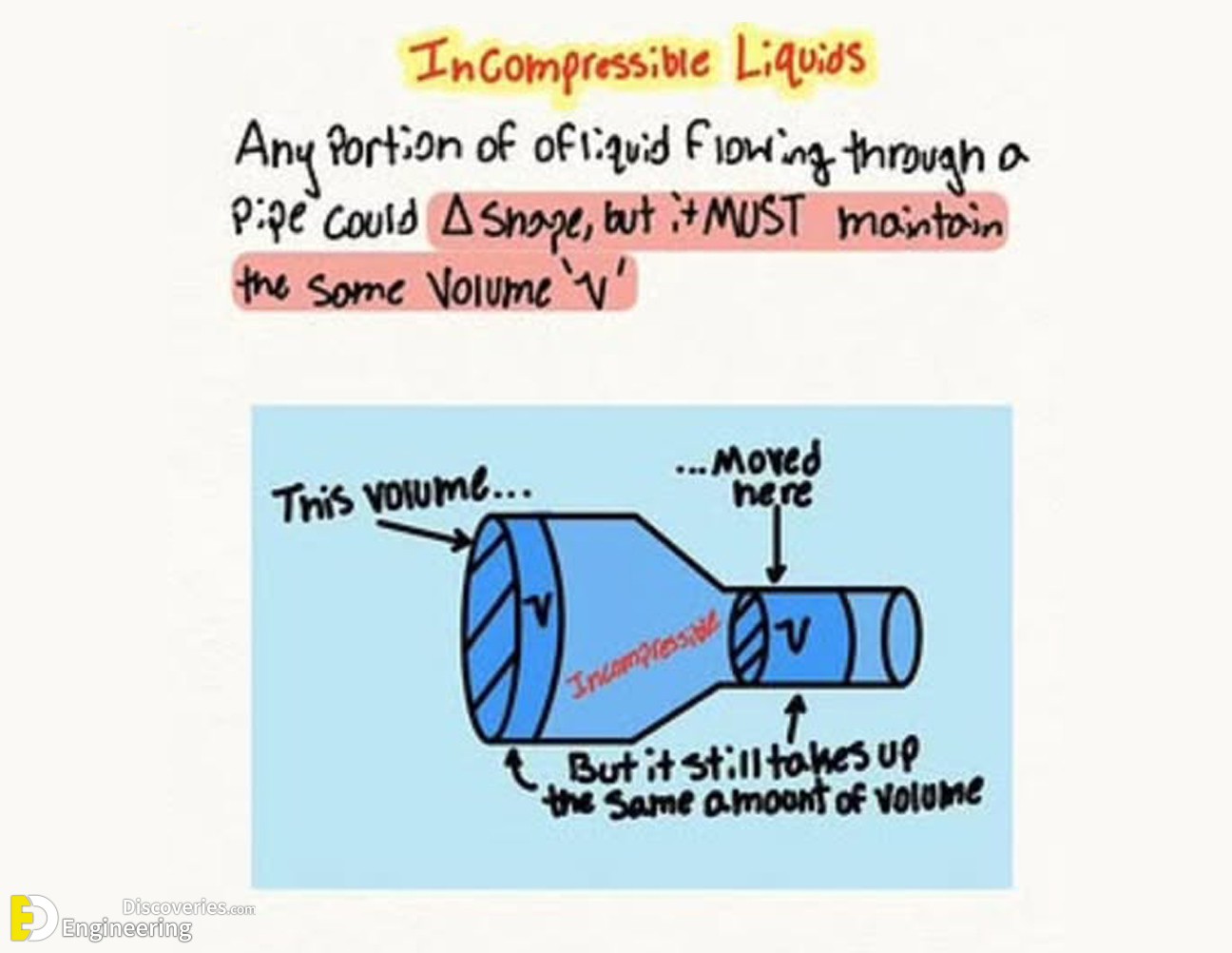
Incompressible Liquids: Maintaining Volume Consistency
In fluid mechanics, an incompressible liquid is one that maintains a constant volume regardless of pressure changes. This means that if a portion of the fluid changes shape, it must still occupy the same volume. This assumption simplifies many fluid dynamic equations and is commonly applied to water and other liquids.
The Continuity Equation: Conservation of Mass in Fluids
The continuity equation ensures that the mass of a fluid remains constant as it flows through a system. It is written as:
A₁ × V₁ = A₂ × V₂
This equation means that if a pipe narrows, the velocity of the fluid must increase to maintain the same flow rate. Similarly, if the pipe widens, the velocity decreases. This principle helps explain why water speeds up when coming out of a nozzle and why airplanes generate lift.
Key Takeaways:
- If the cross-sectional area increases, velocity decreases.
- If the cross-sectional area decreases, velocity increases.
Work and Energy Conservation in Fluids
Bernoulli’s equation derives from the Work-Energy Theorem, which connects kinetic energy, potential energy, and pressure energy in a fluid system:
W = ΔK + ΔU
Where:
- W = Work done by the fluid
- ΔK = Change in Kinetic Energy
- ΔU = Change in Potential Energy
This principle helps calculate energy transformations in fluid motion.
Using Bernoulli’s principle, this simplifies to:
This equation describes how pressure, velocity, and height interact in fluid movement, proving essential in engineering applications like water supply systems and hydraulic machines.
Real-World Applications of Bernoulli’s Principle
- Aviation: Airplane wings are designed to create pressure differences, allowing lift to be generated.
- Plumbing Systems: Water flows efficiently through varying pipe diameters due to pressure changes.
- Medical Devices: Blood flow measurements use Bernoulli’s principle to diagnose heart conditions.
- Sports: The spin of a baseball or soccer ball affects its trajectory due to varying air pressure zones.
Conclusion
Bernoulli’s equation is an essential tool in fluid mechanics, explaining how pressure, velocity, and height influence fluid motion. From aerodynamics to engineering, this principle is fundamental to understanding the behavior of fluids in various applications. By mastering Bernoulli’s equation, we can optimize systems for efficiency and functionality in real-world scenarios.